Albert1
- 1,221
- 0
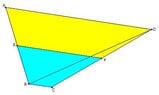
A trapezoid ABCD ,AD // BC ,points E and F are midpoints of AB and CD respectively
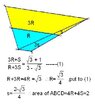
(1)area AEFD :area EBCF =($\sqrt 3+1) : (3-\sqrt 3)$
(2) area of $\triangle ABD=\sqrt 3$
please find the area of ABCD
View attachment 1123
(1)area AEFD :area EBCF =($\sqrt 3+1) : (3-\sqrt 3)$
(2) area of $\triangle ABD=\sqrt 3$
please find the area of ABCD
View attachment 1123
Attachments
Last edited: