Find Area Shaded in Red of Curve f(x)

[MarkFL]

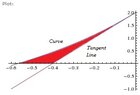
Consider the following diagram:

View attachment 1248

The curve is given by:

\(\displaystyle f(x)=\left(e^x+x \right)\left(e^x+1 \right)\)

The tangent line is tangent to the curve at $x=0$.

Please compute the area shaded in red.

 

[Opalg]

[sp]Let $x_0$ be the point such that $f(x_0) = 0$, so that $e^{x_0} + x_0 = 0$ (because the other factor in $f(x)$ is always positive). The shaded area is given by \(\displaystyle A = \int_{x_0}^0f(x)\,dx - \tfrac25,\) the $\frac25$ being the area of the triangle comprising the unshaded area under the curve. So we have to evaluate $$\int_{x_0}^0f(x)\,dx = \int_{x_0}^0(e^{2x} + (x+1)e^x + x)\,dx = \Bigl[\tfrac12e^{2x} + e^x + \tfrac12x^2\Bigl]_{x_0}^0 = \tfrac12\Bigl[( e^x + x)^2\Bigl]_{x_0}^0 = \tfrac12(1-0) = \tfrac12.$$ Thus $A = \frac12 - \frac25 = \frac1{10}.$[/sp]

 

[MarkFL]

Hello Opalg,

Spot on as always. (Sun)

I used essentially the same method:

Spoiler

This problem was originally posted about a year ago on another forum, and the student was confused by not having a lower limit of integration. He knew zero was the upper limit, but was unable to determine the root of the curve.

He had already determined the equation of the tangent line to be:

\(\displaystyle y=5x+2\)

To see that this is true, we find by differentiating $f$ with respect to $x$:

\(\displaystyle f'(x)=\left(e^x+x \right)e^x+\left(e^x+1 \right)^2\)

Hence, we find:

\(\displaystyle f'(0)=5\)

and then applying the point-slope formula, we have:

\(\displaystyle y-2=5(x-0)\)

\(\displaystyle y=5x+2\)

And so the area under the tangent line and bounded by the axes is a right triangle whose base is the magnitude of the $x$-intercept, or $\dfrac{2}{5}$, and whose altitude is $2$, which means the area under the line is:

\(\displaystyle A_T=\frac{1}{2}\cdot\frac{2}{5}\cdot2=\frac{2}{5}\)

To find the area under the curve, I instructed him to let $x_0$ represent this root, and so we may write:

\(\displaystyle A_C=\int_{x_0}^0 \left(e^x+x \right)\left(e^x+1 \right)\,dx\)

Next, use the substitution:

\(\displaystyle u=e^x+x\,\therefore\,du=\left(e^x+1 \right)\,dx\)

Since $f\left(x_0 \right)=0$, then we must have $e^{x_0}+x_0=0$ as well, because the other factor $e^x+1$ has no real roots. And so our definite integral becomes:

\(\displaystyle A_C=\int_0^1 u\,du=\frac{1}{2}\left[u^2 \right]_0^1=\frac{1}{2}\)

Finally, since the shaded area $A$ is the area under the curve less the area under the tangent line, we may write:

\(\displaystyle A=A_C-A_T=\frac{1}{2}-\frac{2}{5}=\frac{1}{10}\)