- #1
yyttr2
- 46
- 0
ok, I am preparing for a test and I can not find this explained simply online.
how do I find the force of tension on two ropes supporting a box (mg=98N) if the angle that the ropes form are not equal to one another?
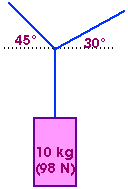
please help? D:
how do I find the force of tension on two ropes supporting a box (mg=98N) if the angle that the ropes form are not equal to one another?
please help? D:
Attachments
Last edited:

