Find ##\frac{dh}{dt}## in the problem involving related change.

[chwala]

Homework Statement

See attached

Relevant Equations

Related change- differentiation.

Find the problem here with solution. My interest is on part (a) only.

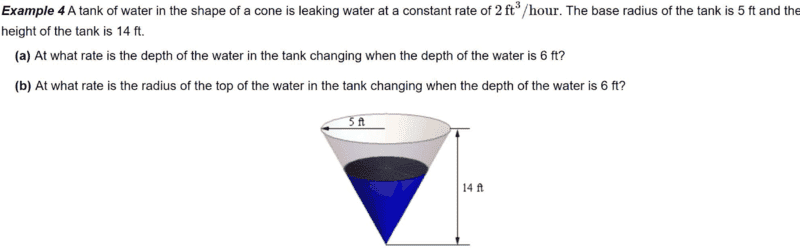Solution;

The steps to solution are very much clear...the author made use of implicit differentiation. Now, would i be right to have;

$\dfrac{dV}{dt}=\dfrac{dV}{dh}\cdot \dfrac{dh}{dt}+ \dfrac{dV}{dr}\cdot \dfrac{dr}{dt}$

$-2=\dfrac{1}{3}π×\left[\dfrac{5}{14} h\right]^2\dfrac{dh}{dt}+\dfrac{2}{3}π ×\left[\dfrac{5}{14} h\right]h\dfrac{dr}{dt}$

We know that $r=\dfrac{5}{14} h,$ therefore $\dfrac{dr}{dt}=\dfrac{5}{14}\dfrac{dh}{dt}$

$-2=\dfrac{1}{3}π×4.5918\dfrac{dh}{dt}+\dfrac{2}{3}π×12.857×\left[\dfrac{5}{14} h\right]h\dfrac{dr}{dt}$

$-2=4.8084\dfrac{dh}{dt}+9.6170\dfrac{dh}{dt}$

$-2=14.4254 \dfrac{dh}{dt}$

$\dfrac{dh}{dt}=-0.1386$

Your thoughts...i hope i did not just go round and round on the implicit approach...but hey that's how i think on this.

 

[Mark44]

The steps to solution are very much clear...the author made use of implicit differentiation. Now, would i be right to have;
$\dfrac{dv}{dt}=\dfrac{dv}{dh}\cdot \dfrac{dh}{dt}+ \dfrac{dv}{dr}\cdot \dfrac{dr}{dt}$
$-2=\dfrac{1}{3}π\cdot \left[\dfrac{5}{14} h\right]^2⋅\dfrac{dh}{dt}+\dfrac{2}{3}π\cdot \left[\dfrac{5}{14} h\right]⋅h⋅\dfrac{dr}{dt}$

Certainly volume V is a function of both r and h, but due to the fact that every vertical cross-section of the cone is a triangle, it's much more convenient (and a lot easier) to treat r as a linear function of h (or vice versa), which makes V a function of a single variable.

Later edit: Another problem with your approach is that you're given neither dr/dt nor dh/dt. In what I described in the previous paragraph, the text you quoted actually gives the linear relationship between h and r; namely, $r = \frac 5{14}h$. By replacing r in the equation for V for the cone, V can be written as a function of h alone.

Nits:

• Your total derivative above, $\dfrac{dv}{dt}$ should be written in terms of the partial derivatives of volume with respect to r and h respectively. That is, in terms of $\frac{\partial V}{\partial r}$ and $\frac{\partial V}{\partial h}$, not as ordinary derivatives.
• Stylewise, V is traditionally used for volume while v (lowercase) is used for velocity.

 

[chwala]

Hey @Mark44 ...i've been busy marking scripts as an Examiner. Hope all well...