- #1
chwala
Gold Member
- 2,753
- 388
- Homework Statement
- See attached.
- Relevant Equations
- ##s=vt##
Find the questions and its solution below;

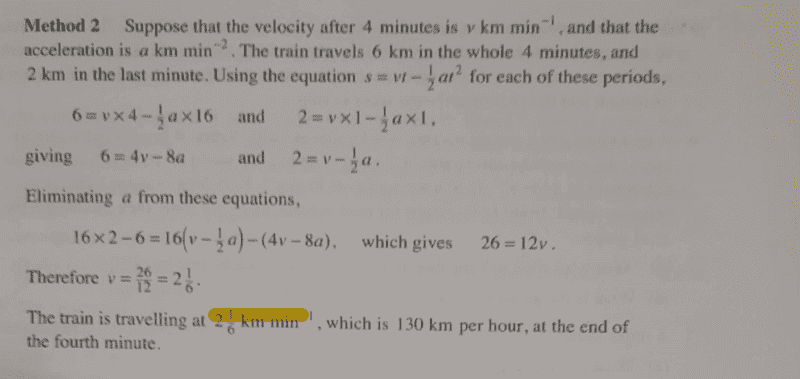
Now would i be correct to use;
##v= u +at## where i considered ##v=33.3##m/s and ##u=16.67##m/s as the given average velocities between the two points in reference. Then it follows that,
##33.33=16.67 + 150a##
##→a= 0.11##
We are told that ##a## is constant throughout... Letting the unknown final velocity (which we are looking for) ##=v_2##, then
using ##v=u+at##
##v_2 = 33.33 +(0.11×30)=33.33+3.3=36.63##m/s
Now would i be correct to use;
##v= u +at## where i considered ##v=33.3##m/s and ##u=16.67##m/s as the given average velocities between the two points in reference. Then it follows that,
##33.33=16.67 + 150a##
##→a= 0.11##
We are told that ##a## is constant throughout... Letting the unknown final velocity (which we are looking for) ##=v_2##, then
using ##v=u+at##
##v_2 = 33.33 +(0.11×30)=33.33+3.3=36.63##m/s

 ##t=120##...oops, therefore,
##t=120##...oops, therefore,