Step 3 is good!
Now let's go over why I believed you were talking out of your backside in your first few posts:
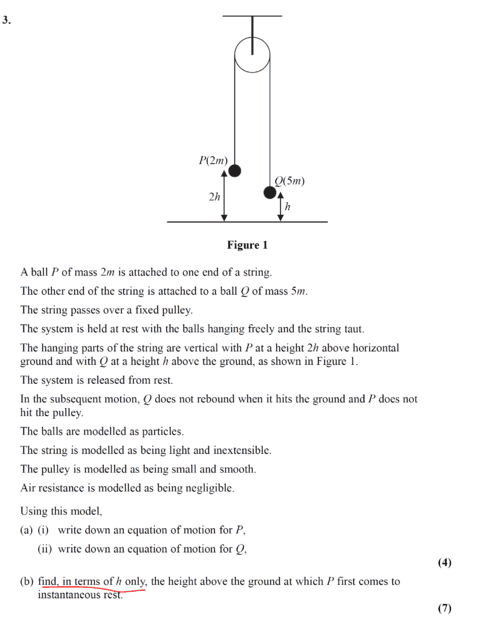
1) No diagram labeling conventions.
2) No visible application of newtons 2nd law - just an answer from the book was presented
3) This quote:" In my understanding, the displacement on either side would be the same, that is ##=h##m given the condition (assumption) that ##a=0##."
What would a= 0 have to do with the displacements? The displacements are tied to the inextensible string condition.
4) You ask if v or v^2 adds any value to the solution with this post!!!
chwala said:
and was this part adding any value to the working to solution?
chwala said:
5) You use the variable ##h## as a general statement! Its a variable specific to the problem. Don't Do That!
chwala said:
we know that upwards acceleration = downwards acceleration and using
##v^2=u^2+ 2gh##
6) You square ##v^2## and square 2gH, just to unsquare it in this part!
chwala said:
I shall have,
##\left(\dfrac{2×3gh}{7}\right)^2 =(2gH)^2##
##\dfrac{2×3gh}{7} =2gH##
##\dfrac{3gh}{7}=gH##
##H=\dfrac{3h}{7}##.
7) In a subsequent post you reveal that you didn't realize P keeps traveling up after Q hits the ground!
chwala said:
Learning point for me. So you are implying that ##P## will continue travelling upwards after ##Q## hits the ground? A distance ##h##? let me check that out.
How do you solve the problem without understanding this...It is simply not possible!
8) Then This: You set ##v = v##.
chwala said:
after ##Q## hits the ground, ##P## will travel,
##0 = -8.4h + 2(4.2)h## distance,
##8.4h =8.4h##
##h=1##
now if this is correct, doe imply that,##h=1##? metres. Cheers.
So there is absolutely no reason for you to make the statement:
chwala said:
This is just but a repitition of my earlier post...
Do we understand each other yet?