Undergrad Find input values for smallest function amplitude

[TheFistGuy]

Hello!

I have a function y(x) with variables a; b; c; d.

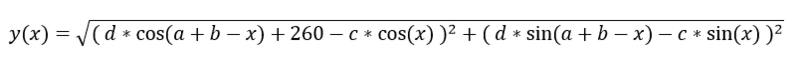
I know what the values of a; b; c; d roughly should be, but I am trying to calculate them precisely, so the graph of the function over the region from a to a+90° would look as straight (horizontal with smallest possible amplitude) as possible.

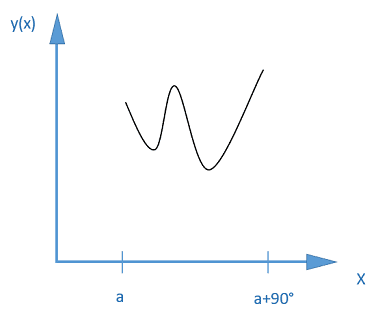
How do I do this? Where do I start?
I haven't done any maths work in years but i still have access to Matlab, Mathematica, Mathcad from my collage days.

Any help greatly appriciated, as I can't find anything on the web, not knowing which keywords (proper terminology) I should be using.

 

[mfb]

c=d=0 makes it exactly flat. Is that really what you want?
What is the actual problem you want to solve?

In general: You can find the highest and lowest point for different (a,b,c,d) and then run a conventional minimization algorithm to find the optimum.

 

[TheFistGuy]

Ahh, I am actually designing a mechanism with some levers and I stumbled upon this problem, which I decided to solve mathematically.

So I know approximate values:
c = 60.0 (plus or minus 1.0)
d = 60.0 (plus or minus 1.0)
a = 22.0° (plus or minus 1.0)
b = 292.0° (plus or minus 1.0)

I am really interested in calculating a,b,c,d with a precision of 0.1, so that the graph would look as flat as possible.

 

[mfb]

While you can do the procedure I suggested I'm highly confident that the result is not what you want. It will almost certainly run into the limits of +- 1, and I guess you'll get c=59, d=59, and I'm not sure if the values for a and b even matter. It won't make the graph notably flatter, and I don't see what you would learn from this mathematical solution.