Find Isobaric Expansion & Pressure-Volume Coefficient for Solid

[member 731016]

Homework Statement

The problem I am trying to solve is,
Find the isobaric expansion coefficient $\frac{dV}{dT}$ and the isothermal pressure-volume coefficient $\frac{dV}{dP}$ of a solid that has equation of state $V+bpT–cT^2=0$

Relevant Equations

Equation of state of solid: $V+bpT–cT^2=0$

The answer to this problem is

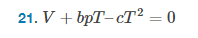
However, I am confused how this relates to the question.

My working is,
$V = cT^2 - bpT$
$\frac{dV}{dT} = 2cT - bp$ (I take the partial derivative of volume with respect to temperature to get the isobaric expansion coefficient)

$\frac{dV}{dP} = 0$ (I take the partial derivative of volume with respect to pressure to get the isothermal pressure-volume coefficient)

If someone please knows whether I am correct or not then that would be greatly appreciated!

Many thanks!

 

[haruspex]

I suspect that p and P are supposed to be the same.

 

[member 731016]

I suspect that p and P are supposed to be the same.

Thank you for your reply @haruspex!

That gives $\frac{dV}{dP} = -bT$. Do you please know whether the textbook solution is wrong? It appears they just give a polynomial in temperature.

Many thanks!

 

[haruspex]

Thank you for your reply @haruspex!

That gives $\frac{dV}{dP} = -bT$. Do you please know whether the textbook solution is wrong? It appears they just give a polynomial in temperature.

Many thanks!

It is obviously not an answer to the question. It merely restates the given equation. The answers must take the form $\frac{dV}{dT}=$ etc. Or better, $\frac{\partial V}{\partial T}=$ etc.
Perhaps the original question was the reverse: it provided the partial derivatives and asked for the state equation. Someone changed the question but forgot to change the answer.

 

[member 731016]

It is obviously not an answer to the question. It merely restates the given equation. The answers must take the form $\frac{dV}{dT}=$ etc. Or better, $\frac{\partial V}{\partial T}=$ etc.
Perhaps the original question was the reverse: it provided the partial derivatives and asked for the state equation. Someone changed the question but forgot to change the answer.

Thank you for your help @haruspex ! I understand now :)