Find Lambda Baryon Decays Cross Section Ratio

[Xylios]

I've been asked to find the ratio between the cross sections of the two folowing decais:

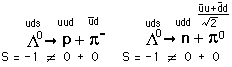
Using the CKM matrix and the feynman diagrams for both decays, I reach the conclusion that the Ratio is exactly 1. However, consulting this document,

http://pdg.lbl.gov/2012/tables/rpp2012-tab-baryons-Lambda.pdf

We clearly see it is not. I do not understand where the problem lies.

My reasoning is the following:
- The decays are exactly the same, except for the final arrangement of the quarks
- Since the vertices are the same, the probability of each interaction is the same in both cases.
- Since the probabilities are the same, the interaction rates are the same.
- Since the mass of the products is roughly equal in both cases, the density of final states is the same
- The cross section is the same.

 

[Vanadium 50]

Two words: Clebsch-Gordon

 

[Xylios]

Two words: Clebsch-Gordon

Are you talking about the fact that the neutral pion is in fact a superposition of two mesons? I thought about that, but I do not understand how I can insert that into Fermi's golden rule and obtain the experimental result.

 

[Xylios]

Ok, after searching for a couple hours I think I found it:

We have a final state with I=1/2 and I3=-1/2. This state is a linear combination of |n, pi0)=|1/2,-1/2)x|1,0) and |p, pi-)=|1/2,1/2)x|1,-1). Therefore, to find the ratio between branches we just need to find a ratio between the coefficients of the linear combination which are the Clebsch-Gordan coefficients.

Is that it?

 

[vanhees71]

Two words: Clebsch-Gordon

Clebsch-Gordan

 

[Vanadium 50]

Got me on that one!

 

[samalkhaiat]

Is that it?

Yes, provided you know what all that has to do with the weak decay. Once you “choose” the final state, $|N \pi \rangle$, to be $|1/2 , -1/2\rangle$, you are done: The Clebsch-Gordan expansion gives you
$$| p \pi^{-} \rangle = \sqrt{1/3} \ | \frac{3}{2} , - \frac{1}{2} \rangle - \sqrt{2/3} \ |\frac{1}{2} , - \frac{1}{2} \rangle ,$$
$$|n \pi^{0} \rangle = \sqrt{2/3} \ | \frac{3}{2} , - \frac{1}{2} \rangle + \sqrt{1/3} \ |\frac{1}{2} , - \frac{1}{2} \rangle .$$
Solving these for “the final state”, you get
$$|\frac{1}{2} , -\frac{1}{2} \rangle = -\sqrt{2/3} \ |p \pi^{-} \rangle + \sqrt{1/3} \ |n \pi^{0} \rangle .$$
From this you obtain the result
$$\frac{\sigma \left( \Lambda \to p\pi^{-}\right)}{\sigma \left( \Lambda \to n\pi^{0}\right)} = \frac{(-\sqrt{2/3})^{2}}{(\sqrt{1/3})^{2}} = 2 ,$$ which agrees with the experimental data very well.
Okay, now here are my questions to you:
1) In the final state $|N\pi \rangle$, the nucleon has $I_{N}=\vec{1/2}$ and the pion has $I_{\pi} = \vec{1}$. Therefore, the final state must have $I_{N\pi} = \vec{3/2}$ or $\vec{1/2}$. So, what made you “choose” $|\frac{1}{2} , -\frac{1}{2} \rangle$ to be the final state? What is wrong with the state $|\frac{3}{2} , -\frac{1}{2} \rangle$?
2) Closely related to (1) is the question about the initial state $|\Lambda \rangle$, which we know it is an iso-singlet $|0 , 0\rangle$: In order to find $\sigma (\Lambda \to N\pi)$, we need to evaluate the matrix elements $$T(\Lambda \to N\pi) = \langle N \pi | \mathcal{H}^{|\Delta S| = 1}| \Lambda \rangle ,$$ where $\mathcal{H}^{|\Delta S| = 1}$ is the low energy (non-leptonic) weak Hamiltonian. So, where is the initial state in the above mentioned analysis? Why was there no mention of the initial state $|\Lambda \rangle$?
If you know the answers to those questions, you are okay. Otherwise, you will have to ask better questions.