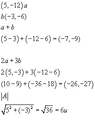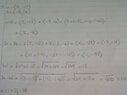Find $\left| a-b \right|$: Vectors and Magnitude

[ineedhelpnow]

find $a+b, 2a+3b, \left| a \right|, \left| a-b \right|$

$a=\left\langle 5,-12 \right\rangle$
$b=\left\langle -3,-6 \right\rangle$

ive found all of them except the last one. how to do i find $\left| a-b \right|$

 

[ineedhelpnow]

nvm i got it. answer's 10.

 

[leprofece]

Ok this is my first question to answer
In a+b we sum components to components to get the result in tthe image

in 2a + 3b we multiply a by 2 y b by 3 then we aplly the methods of exercise 1

in A module we apply the pitagoprean formula to get the sqrt 36 = 6
View attachment 2978
Any observations please let me know
oh yes Module A is sqrt(5^2 + 12 ^2) = sqrt(169) = 13

 

[ineedhelpnow]

here's what i did :) sorry for my handwriting. i did the problem real quick so it came out kind of sloppy. it should be right because that's what the back of my book has for answers.
View attachment 2979

 

[ineedhelpnow]

you got a bit mixed up with the signs on the a+b and with 2a+3b there was a bit of confusion with what's a and b ;) but i think OVERALL we have the same idea in our steps :) thanks for your help though

 

[Prove It]

here's what i did :) sorry for my handwriting. i did the problem real quick so it came out kind of sloppy. it should be right because that's what the back of my book has for answers.
View attachment 2979

Since when is -12 + (-6) equal to -6?

 

[ineedhelpnow]

since i dropped my brain and forgot to pick it up

- - - Updated - - -

actually my mistake there was that i put -(-6) instead of +(-6). if it were the other way i would be right :)