- #1
Albert1
- 1,221
- 0
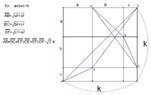
$a,b,c>0$
$a+b+c=k$
find:$min(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2})$
$a+b+c=k$
find:$min(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2})$