dcmf
- 16
- 5
- Homework Statement
- Two equal mass blocks are initially at rest and sitting on a frictionless surface. A hand exerts a force of magnitude F on block A, which pushes it to the right by a distance d. Another hand exerts of force of the same magnitude F on block B, which pushes it to the left the same distance d. Consider the blocks A and B as the system. Is the sign of the net external work (Wext) done
by the hands on the system positive, negative, or is it zero?
- Relevant Equations
- W = Fdcosθ, K = 1/2mv^2, E1+W = E2
A diagram is also provided, which looks like this:
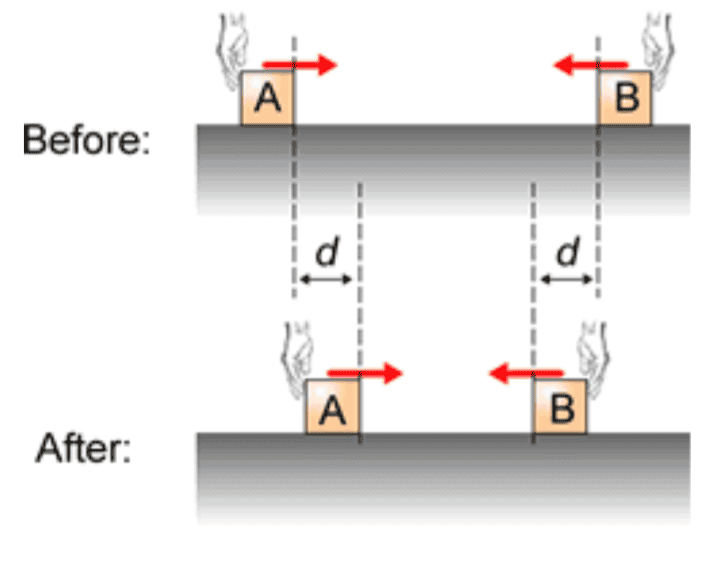
I'm not sure what is correct and after doing some digging online I still haven't been able to come to a consensus. I'm currently stuck between one of two possibilities: positive or zero. I'm pretty sure work on A (Wa) and work on B (Wb) are each positive values (force in same direction as displacement, right??). I also think I getting bogged down by the term "net external work (Wext)" since I'm not 100% sure what this indicates.
Why it might be positive:
If Wa and Wb are positive and Wext is the net external work, I feel like you should be able to just sum up Wa and Wb - making Wext a positive value. Work is a scalar quantity too so there shouldn't be issues with directions being associated with the signs.
Why it might be zero:
At the same time, intuitively it feels like if you consider system A+B, Wa and Wb would cancel each other out somehow because the forces and displacements are equal and opposite to each other. Also would energy equations be valid here (e.g. E1+W = E2) since you're moving the blocks from rest?
I'm not sure what is correct and after doing some digging online I still haven't been able to come to a consensus. I'm currently stuck between one of two possibilities: positive or zero. I'm pretty sure work on A (Wa) and work on B (Wb) are each positive values (force in same direction as displacement, right??). I also think I getting bogged down by the term "net external work (Wext)" since I'm not 100% sure what this indicates.
Why it might be positive:
If Wa and Wb are positive and Wext is the net external work, I feel like you should be able to just sum up Wa and Wb - making Wext a positive value. Work is a scalar quantity too so there shouldn't be issues with directions being associated with the signs.
Why it might be zero:
At the same time, intuitively it feels like if you consider system A+B, Wa and Wb would cancel each other out somehow because the forces and displacements are equal and opposite to each other. Also would energy equations be valid here (e.g. E1+W = E2) since you're moving the blocks from rest?