Find path to minimum cost from start to finish

[mathmari]

Hey!

I am looking the following:
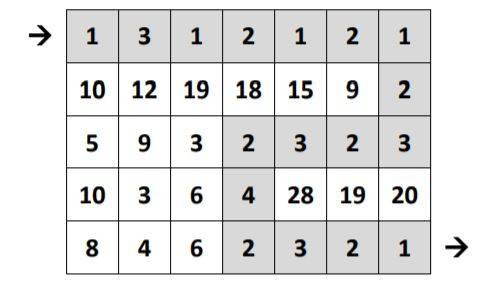
The board of a game is an $M \times N$ board with squares, where the starting point is on left - in position $(0, 0)$ - and the finish is in the lower right - in position $(M-1, N-1)$. Each square contains a positive number that describes the cost of moving to pass through this specific square. Design and analyze an algorithm that finds the path to minimum cost from start to finish considering that we can move up, down, right or left. For example, in the table below the minimum cost is 35 and is given by the designed path.

For this problem I have the following idea:

We convert this table into a graph, specifically a weighted graph with weights the cost of each square. In this way the problem will be to find the shortest path of the graph, right? :unsure:

That graph that we get is not directed, is it? :unsure:

 

[I like Serena]

Hey mathmari!

Yep. That will work. (Nod)

Suppose we move from square (0,0) to (0,1), what will be the weight that we assign to this path?
And what is the weight if we move from (0,1) to (0,0)?

 

[mathmari]

Suppose we move from square (0,0) to (0,1), what will be the weight that we assign to this path?

Isn't it equal to $1+3=4$ ? :unsure:

And what is the weight if we move from (0,1) to (0,0)?

Isn't it $3=1=4$ ? :unsure:

Suppose we are at the point $(i,j)$ then the possible moves are up, left , right, down, i.e to go to $(i-1,j)$, $(i,j-1), (i,j+1), (i+1, j)$, right? :unsure:

So for the pseudocode, do we get the following?

    Algorithm Minimum_Cost_Path
       Input: Numbers M, N, Set S of number of each square (i,j) on board
       Output: Minimum Cost Path from (0,0) to (M-1, N-1)
        G <- new empty graph
        for i <- 0 to M-1 do
              for j <- 0 to N-1 do
                    G.AddVertex( (i,j) )
        for i <- 0 to M-1 do
              for j <- 0 to N-1 do
                    G.AddEdge( (i,j), (i-1,j), S( i-1,j ) ) 
                    G.AddEdge( (i,j), (i,j-1), S( i,j-1 ) ) 
                    G.AddEdge( (i,j), (i,j+1), S( i,j+1 ) ) 
                    G.AddEdge( (i,j), (i+1,j), S( i+1,j ) )

Now we have created the graph, right? Is that correct so far? :unsure:

Now we far to call an algorithm that calculates a shortest path. Do we apply Dijkstra because we have only positive weights and we are looking for a path between two specific vertices? :unsure:

 

[I like Serena]

Isn't it equal to $1+3=4$ ?
Isn't it $3=1=4$ ?

Doesn't that mean that if we follow (0,0) -> (0,1) -> (0,0) that we get a weight of (1+3)+(3+1)=8?
That is, aren't we counting the 3 twice when we should only count it once?

What I mean, is that I believe we need a directed graph, which is actually what you implemented in your algorithm.

Suppose we are at the point $(i,j)$ then the possible moves are up, left , right, down, i.e to go to $(i-1,j)$, $(i,j-1), (i,j+1), (i+1, j)$, right?

Now we have created the graph, right? Is that correct so far?

Shouldn't we consider that not every edge is possible since some of the destinations are "off the board"?

Btw, don't forget to keep track of the starting and ending vertices in G.

Now we far to call an algorithm that calculates a shortest path. Do we apply Dijkstra because we have only positive weights and we are looking for a path between two specific vertices?

Yep. (Nod)

 

[topsquark]

I don't know how to apply the programming that well anymore but what if there is a path that goes 1, 4, 1, 1, .. that is the actual lowest cost? Your algorithm wouldn't find that, would it? Your path finds the lowest cost by adding the lowest cost at each step, not necessarily the lowest path on the board.

-Dan

 

[mathmari]

Doesn't that mean that if we follow (0,0) -> (0,1) -> (0,0) that we get a weight of (1+3)+(3+1)=8?
That is, aren't we counting the 3 twice when we should only count it once?

What I mean, is that I believe we need a directed graph, which is actually what you implemented in your algorithm.

I haven't really understood how it follows that the graph has to be directed. Could you explain that further to me? :unsure:

Shouldn't we consider that not every edge is possible since some of the destinations are "off the board"?

Ahh sowe have to consider some restrictions if the point is on the edges, right? :unsure:

Btw, don't forget to keep track of the starting and ending vertices in G.

What do you mean? :unsure:

 

[mathmari]

I don't know how to apply the programming that well anymore but what if there is a path that goes 1, 4, 1, 1, .. that is the actual lowest cost? Your algorithm wouldn't find that, would it? Your path finds the lowest cost by adding the lowest cost at each step, not necessarily the lowest path on the board.

What do you mean? Do you mean that we consider the best solution in each step and not the best solution in total? :unsure:

 

[topsquark]

What do you mean? Do you mean that we consider the best solution in each step and not the best solution in total? :unsure:

Exactly.

(I got this new scanner/printer because my old one was too fussy. I still can't scan to a file! Anyway.)

Say we have a route counter-clockwise around the left hand lower corner that goes 1, 4, 1, 1, 1, 1, 1, 2, 3, 2, 1. This has a lower cost than the route given in the original problem. The given algorithm wouldn't find it.

-Dan

 

[I like Serena]

I haven't really understood how it follows that the graph has to be directed. Could you explain that further to me?

Consider the board
$$\to\begin{array}{|c|c|c|}\hline 1 & 2 & 3 \\ \hline\end{array}\to$$

The corresponding graph could be:

right?
Also note that it has special nodes for start and finish that we need for Dijkstra's algorithm.

Ahh sowe have to consider some restrictions if the point is on the edges, right?

Yes. We should for instance only add the edge from $(i,j)$ to $(i-1,j)$ if $i>0$.

 

[I like Serena]

Exactly.

(I got this new scanner/printer because my old one was too fussy. I still can't scan to a file! Anyway.)

Say we have a route counter-clockwise around the left hand lower corner that goes 1, 4, 1, 1, 1, 1, 1, 2, 3, 2, 1. This has a lower cost than the route given in the original problem. The given algorithm wouldn't find it.

-Dan

Note that the algorithm as given is incomplete.
Dijkstra's shortest path algorithm still needs to be added to it.
That algorithm will find the shortest path.

 

[mathmari]

Consider the board
$$\to\begin{array}{|c|c|c|}\hline 1 & 2 & 3 \\ \hline\end{array}\to$$

The corresponding graph could be:
View attachment 10853
right?
Also note that it has special nodes for start and finish that we need for Dijkstra's algorithm.

Do you mean that if we has an undirected graph we could go back to "start" ? :unsure:

Yes. We should for instance only add the edge from $(i,j)$ to $(i-1,j)$ if $i>0$.

So do we have the following?

   Algorithm Minimum_Cost_Path
       Input: Numbers M, N, Set S of number of each square (i,j) on board
       Output: Minimum Cost Path from (0,0) to (M-1, N-1)
        G <- new empty graph
        for i <- 0 to M-1 do
              for j <- 0 to N-1 do
                    G.AddVertex( (i,j) )
        for i <- 0 to M-1 do
              for j <- 0 to N-1 do
                    if i>0 then
                          G.AddEdge( (i,j), (i-1,j), S( i-1,j ) )
                    if j>0 then
                          G.AddEdge( (i,j), (i,j-1), S( i,j-1 ) )
                    if j<N-1 then
                          G.AddEdge( (i,j), (i,j+1), S( i,j+1 ) )
                    if i<M-1 then
                          G.AddEdge( (i,j), (i+1,j), S( i+1,j ) )

Then do we just call the algorithm "Dijkstra" ? Or do we have to do also something else? :unsure:

 

[I like Serena]

Do you mean that if we has an undirected graph we could go back to "start" ?

No. (Shake)
The weights as given in the table are for the nodes themselves, and counted when we pass through them.
But for Dijkstra's algorithm we need a graph that assigns weights to the edges instead of the nodes.
In my suggested graph we've solved that problem by assigning the weight of the node we enter to an edge.
It does mean that the reverse edge has a different weight.
And it also means we have to introduce an artificial start node so we can introduce an edge with the weight of the first node.

So do we have the following?

Then do we just call the algorithm "Dijkstra" ? Or do we have to do also something else?

Yes.
And indeed, the only left is to call Dijkstra's algorithm with the graph, the source, and the target. (Nod)

Strictly speaking, we should strip an artificial start node again though (assuming we added one).
Or alternatively, we could choose not to add a start node at all, but instead add the weight of the first node to the result afterwards.

 

[mathmari]

Strictly speaking, we should strip an artificial start node again though (assuming we added one).
Or alternatively, we could choose not to add a start node at all, but instead add the weight of the first node to the result afterwards.

For the first option:

   Algorithm Minimum_Cost_Path
       Input: Numbers M, N, Set S of number of each square (i,j) on board
       Output: Minimum Cost Path from (0,0) to (M-1, N-1)
        G <- new empty graph 
        G.AddVertex(s) // Do we add in that way the artificial starting node? 
        for i <- 0 to M-1 do
              for j <- 0 to N-1 do
                    G.AddVertex( (i,j) )         
        G.AddEdge( s, (0,0), 1 ) // Do we add in that way the weight of that artificial starting node? 
        for i <- 0 to M-1 do
              for j <- 0 to N-1 do
                    if i>0 then
                          G.AddEdge( (i,j), (i-1,j), S( i-1,j ) )
                    if j>0 then
                          G.AddEdge( (i,j), (i,j-1), S( i,j-1 ) )
                    if j<N-1 then
                          G.AddEdge( (i,j), (i,j+1), S( i,j+1 ) )
                    if i<M-1 then
                          G.AddEdge( (i,j), (i+1,j), S( i+1,j ) ) 
        Dijkstra(G, s) // We give here the artificial starting node as input, or not?

:unsure:

 

[I like Serena]

That would work yes.
However, Dijkstra(G, s) does not return a minimum cost path from s to (M-1, N-1).
Instead it returns an array of distances together with an array of "prev" nodes, as explained here on wiki.
Immediately after the algorithm, it also shows what to do if we are only interested in the shortest path to some target node.
That is the path that we want to return from our algorithm, preferably excluding the artificial start node that we added.

So we could do for instance:

(dist, prev) ← Dijkstra(G, s)

P ← empty sequence
u ← G.vertex( (M-1,N-1) )
while u != s
    insert u at the beginning of P
    u ← prev[u]
return P

:unsure:

 

[mathmari]

That would work yes.
However, Dijkstra(G, s) does not return a minimum cost path from s to (M-1, N-1).
Instead it returns an array of distances together with an array of "prev" nodes, as explained here on wiki.
Immediately after the algorithm, it also shows what to do if we are only interested in the shortest path to some target node.
That is the path that we want to return from our algorithm, preferably excluding the artificial start node that we added.

So we could do for instance:

(dist, prev) ← Dijkstra(G, s)

P ← empty sequence
u ← G.vertex( (M-1,N-1) )
while u != s
    insert u at the beginning of P
    u ← prev[u]
return P

:unsure:

This is a code to print the path that we get from Dijkstra, right?

So we could use also the following code, right?

Algorithm print_path(G, s, v, pred)
     if s == v then
           print(s)
     else if pred[v] == -1 then
           print(“No path from s to v")
     else
           print_path(G, s, pred[v], pred)
           print(v)

As for the complexity:

From the nested for loops we get $O(MN)$.
The "G.AddVertex" and "G.AddEdge" are of constant complexity, aren't they?
From Dijkstra we get $O((|V|+|E|)\log(|V|)$ with $|V|=MN$, right? Is $|E|$ also $MN$ ?
The printing part is again of constant complexity, isn't it?

:unsure:

 

[I like Serena]

This is a code to print the path that we get from Dijkstra, right?

So we could use also the following code, right?

Yes and yes.
However, your code prints the path in reverse order, which does not seem to be consistent with the specification of your algorithm.

As for the complexity:

From the nested for loops we get $O(MN)$.
The "G.AddVertex" and "G.AddEdge" are of constant complexity, aren't they?
From Dijkstra we get $O((|V|+|E|)\log(|V|)$ with $|V|=MN$, right? Is $|E|$ also $MN$ ?
The printing part is again of constant complexity, isn't it?

Yes.
Each node has at most 4 edges, so $|E|=O(4MN)$.
The printing part iterates through each of the nodes on the shortest path.
In a worst case scenario that means we have to iterate through $O(MN)$ nodes.

 

[mathmari]

However, your code prints the path in reverse order, which does not seem to be consistent with the specification of your algorithm.

So to get the correct order with this code, do we add the vectors in an array and print them at the end? :unsure:

Each node has at most 4 edges, so $|E|=O(4MN)$.
The printing part iterates through each of the nodes on the shortest path.
In a worst case scenario that means we have to iterate through $O(MN)$ nodes.

So is the total complexity as follows?

Let $c$ be the constant complexity of "G.AddVertex" and $d$ the constant complexity of "G.AddEdge".

\begin{align*}T&=c+ \sum_{i=0}^{M-1}\sum_{j=0}^{N-1}c+d+\sum_{i=0}^{M-1}\sum_{j=0}^{N-1}d+T_{\text{Dijkstra}}+T_{\text{print}} \\ & =c+ \sum_{i=0}^{M-1}\sum_{j=0}^{N-1}c+d+\sum_{i=0}^{M-1}\sum_{j=0}^{N-1}d+O((MN+4MN)\log(MN))+O(MN)
\\ &=c+cMN+d+dMN+O((MN)\log(MN))+O(MN)\\ & =O((MN)\log(MN))\end{align*} Is the analysis correct and complete? :unsure:

 

[I like Serena]

So to get the correct order with this code, do we add the vectors in an array and print them at the end?

That would work yes. (Nod)
You did mean nodes instead of vectors didn't you?

So is the total complexity as follows?

Is the analysis correct and complete?

Yep. (Nod)

 

[mathmari]

That would work yes. (Nod)
You did mean nodes instead of vectors didn't you?

Ah yes!

Do we do that as follows?

Algorithm print_path(G, s, v, pred)
     if s == v then
           Add s at the beginning of the set P 
     else if pred[v] == -1 then
           print(“No path from s to v")
     else
           print_path(G, s, pred[v], pred)
           Add s at the beginning of the set P 
     return P

:unsure:

 

[I like Serena]

Ah yes!

Do we do that as follows?

Algorithm print_path(G, s, v, pred)
     if s == v then
           Add s at the beginning of the set P
     else if pred[v] == -1 then
           print(“No path from s to v")
     else
           print_path(G, s, pred[v], pred)
           Add s at the beginning of the set P
     return P

A set has no ordering. Shall we make it a sequence P instead of a set P?

The name print_path is not accurate any more is it? It's generally not printing.

Suppose the shortest path is $s\to n \to t$, then we get pred[t]=n and pred[n]=s.
I believe the sequence $(s, s, s)$ is returned then, isn't it?
That does not look correct. (Shake)