Find Permutability of Matrices: Algebra Homework Help

  • Thread starter esmeco
  • Start date
  • Tags
    Matrices
In summary, the conversation discusses the concept of exchangeable and permutable matrices. The person is seeking help in finding the set of permutable matrices and clarifies that a matrix is permutable if all rows and columns are the same and if it is a square matrix. However, there is confusion about the definition of exchangeable and permutable.
  • #1
esmeco
144
0
I have this question as homework from my Algebra class:
A square matrix X is called exchangeable with A if AX=XA.Determine the set of permutable matrices with
matrix.jpg


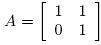
My question is,how do I find that set?I know that a matrix to be permutable all rows and columns must be the same and that a square matrix is composed by the same number of rows and columns.
Thanks in advance for the help!
 
Physics news on Phys.org
  • #2
You defined exchangable, not permutable, so who knows?
 
  • #3
By exchangeable i meant permutable...
 
  • #4
You defined what it means for X to be exchachangable *with A*, not what it means for X to be exchangable, or permutable.
 

FAQ: Find Permutability of Matrices: Algebra Homework Help

What is the definition of permutability of matrices?

Permutability of matrices refers to the ability to rearrange the elements of a matrix without changing its overall structure or properties. In other words, if two matrices can be transformed into each other through a series of row or column swaps, they are considered to be permutable.

How do you determine if two matrices are permutable?

To determine if two matrices are permutable, you can use the commutative property of matrix multiplication. If the product of the two matrices remains the same regardless of the order of multiplication, then the matrices are permutable. This means that the matrices can be rearranged without changing the result of the multiplication.

What is the significance of finding the permutability of matrices?

Finding the permutability of matrices is important in various applications of linear algebra, such as in solving systems of linear equations, computing determinants, and calculating eigenvalues. It also helps in simplifying calculations and reducing the number of steps needed to solve certain problems.

Can all matrices be permuted?

No, not all matrices can be permuted. For two matrices to be permutable, they must have the same dimensions. This means that the number of rows and columns must be the same for both matrices. Additionally, the matrices must have the same number of elements in each row and column.

How can I find the permutability of matrices?

To find the permutability of matrices, you can use various techniques such as finding the transpose, calculating the determinant, or performing matrix operations. These methods can help determine the similarity or equivalence of two matrices, which in turn, can indicate their permutability.

Similar threads

Linear Algebra - Elimination Matrix when Permutation Needed
Replies
2
Views
1K
Proving statements about matrices | Linear Algebra
Replies
25
Views
3K
Getting identity out of a finite number of permutaions
Replies
7
Views
1K
Find the sampling matrix and sampling structure for R, G and B components
Replies
2
Views
2K
Mastering Combinatorics: Exploring the Formula for Permutations
Replies
1
Views
915
Prove that a matrix can be reduced to RRE and CRE
Replies
4
Views
2K
[Linear Algebra] Maximal linear independent subset
Replies
3
Views
2K
A gardener collected 17 apples...
Replies
32
Views
1K
Given specific v, dimension of subspace of L(V, W) where Tv=0?
Replies
15
Views
2K
Linear Algebra, Find a matrix C st CA = B
Replies
2
Views
3K

Hot Threads

Recent Insights

Back
Top