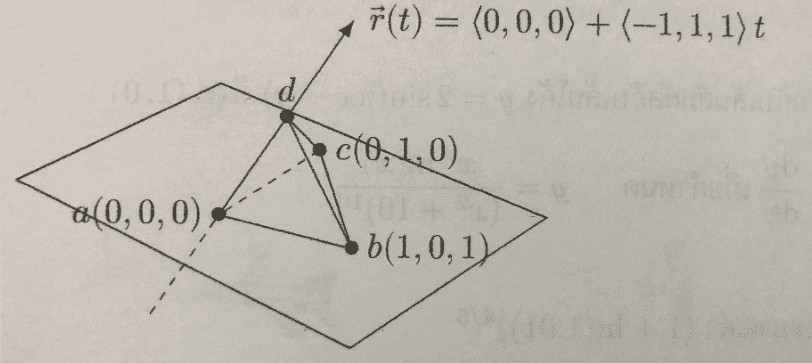Find Point D on Plane for 4 Unit Cube Pyramid

[jaychay]

Find point d on the line of r(t)=(0,0,0)+(−1,1,1)t which make the triangular pyramid abcd has the volume of 4 unit cube when a(0,0,0),b(1,0,1),c(0,1,0) are the points on the plane of −x+z=0.

 

[I like Serena]

The area $B$ of the base rectangular triangle $\Delta abc$ is $B=\frac 12\cdot ab\cdot ac = \frac 12 \sqrt 2\cdot 1$.
The volume of the pyramid is $V=\frac 13 Bh$, where $B$ is the area of the base, and $h$ is the height perpendicular to the base.
The normal vector $\vec n$ of the plane can be deduced from its equation $-x+z=0$, meaning it is $\vec n=(-1,0,1)$.
The height $h$ of the pyramid is the projection of the vector $\overrightarrow{ad}$ onto the normal vector $\vec n$.
The formula for that projection is $h=\frac{\overrightarrow{\mathstrut ad} \cdot \overrightarrow{\mathstrut n}}{\|\vec n\|}$.

So we have:
$$\begin{cases}B=\frac 12\sqrt 2 \\
V=\frac 13 Bh = 4 \\
\vec n = (-1,0,1) \\
h=\frac{\overrightarrow{\mathstrut ad} \cdot \overrightarrow{\mathstrut n}}{\|\vec n\|} = \frac{(-1,1,1)t \cdot (-1,0,1)}{\|(-1,0,1)\|} = \frac{2}{\sqrt 2}t=t\sqrt 2
\end{cases}
\implies V = \frac 13 \cdot \frac 12\sqrt 2 \cdot t\sqrt 2 = 4
\implies t = 12
$$
So point $d$ is $(0,0,0)+(-1,1,1)12=(-12,12,12)$.

 

[jaychay]

Thank you very much !

 

[skeeter]

I learned (long ago) this formula for the distance from a point, $(x_1,y_1,z_1)$ to a plane $Ax+By+Cz+D = 0$

$d = \dfrac{|Ax_1+By_1+Cz_1+D|}{\sqrt{A^2+B^2+C^2}}$

$V = \dfrac{Bh}{3} = \dfrac{1}{\sqrt{2}} \cdot \dfrac{h}{3} = 4 \implies h = 12 \sqrt{2}$

$12\sqrt{2} = \dfrac{|-1(-t) + 0(t) + 1(t) + 0|}{\sqrt{(-1)^2 + 0^2 + 1^2}}$

$12\sqrt{2} = \dfrac{2t}{\sqrt{2}} \implies t = 12$