Find Side AB of Triangle ABC Given M, N, and C

[Wilmer]

                     B
 

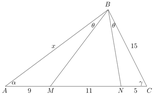
                              15

 
A     9     M        11        N   5   C

Triangle ABC, BC = 15, AC = 25.
M and N on AC, such that AM = 9, MN = 11 and CN = 5.
Angle ABM = angle CBN.
Calculate side AB.

 

[pickslides]

It seems as simple as x/9 = 15/5, or am I missing something?

 

[Wilmer]

It seems as simple as x/9 = 15/5, or am I missing something?

No; those 2 triangles are not similar...and solution NOT simple: guaranteed!

 

[Evgeny.Makarov]

It seems as simple as x/9 = 15/5, or am I missing something?

Are you claiming that triangles ABM and NBC are similar? Also, it is strange that the fact MN = 11 is not used.

 

[Opalg]

View attachment 161

From the sine rule in triangle BNC, $\dfrac{\sin\theta}5 = \dfrac{\sin(\theta+\gamma)}{15}$.

From the sine rule in triangle BMA, $\dfrac{\sin\theta}9 = \dfrac{\sin(\theta+\alpha)}x$.

From the sine rule in triangle ABC, $\dfrac{\sin\alpha}{15} = \dfrac{\sin\gamma}x = \dfrac{\sin(\alpha+\gamma)}{25}$.

That gives four equations for the four unknowns $x$, $\theta$, $\alpha$, $\gamma$. So all you have to do is to solve the equations to find $x$.

In practice, I struggled to do that, but eventually I managed to eliminate $x$ and $\theta$ from the equations and ended with the relation $\sin\alpha = \tfrac23\sin\gamma.$ From there, it was easy to conclude that $\boxed{x = 22.5}.$ (Also, $\cos\alpha = \tfrac{29}{36}$, $\cos\gamma = \tfrac{11}{24}$ and $\tan\theta = \tfrac{\sqrt{455}}{61}.$)

 

[Wilmer]

Yep. There is a much easier solution using: A(0,0), C(25,0), B(x,y).
G on AC such that BG perpendicular to AC: AG = x, BG = y (of course).
Let u = angleABM = angleCBN.

TriangleABM: TAN(u) = [y / (x-9) - y/x] / [1 + (y / (x-9))(y/x)]
Do similarly with triangleBCN.
Use above equality and, along with Pythagoras' help with rights ABG and CBG, solve.