Find starting velocity from golfer launching ball

[bremenfallturm]

Homework Statement

A golfer attempts an "hole in one" by launching the ball at an initial velocity $v_0$, making a $30^\circ$ angle with the golf course. The golf course makes an angle $\alpha$ with the horizontal. Find the initial velocity of the ball, given that the distance to the hole along the golf course is $l$. Find numerical values for $v_0$, if $l=20m$ and $\alpha = 10^\circ$

Relevant Equations

$$
\sum \vec F = m\vec a
$$

Hello! Hope I got this right. Completely new around here.
The image that goes along with the problem is:

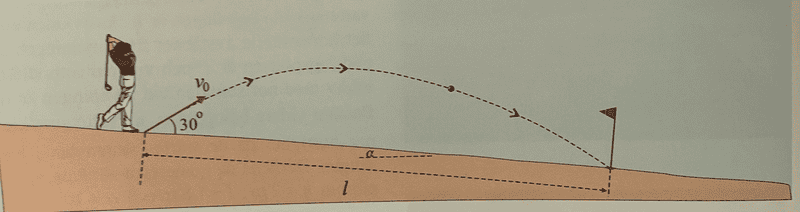
What I have tried so far can be found below:

I do not know if it is a computational error or a physics error, but I tried using WolframAlpha to solve for $v_0$ to validate and did not get the answer that my book suggests:
$$v_0 = \sqrt{\frac{2gl\cos \alpha}{\tan \alpha + \sqrt 3}}$$
What am I doing wrong? The physics or the math?

 

[bremenfallturm]

I can clarify that I got (2) from solving the equation $y=0$. Looks like it wasn't crystal clear in my solution.

 

[Hill]

In

the second term should have $v_0^2$.

 

[kuruman]

Problems of this sort can be solved quite easily if you write the displacement vector $\mathbf L$ as the sum of two vectors and draw the vector addition diagram (see right) $$\mathbf L=\mathbf v_0~t_{\!f}-\frac{1}{2}\mathbf g t_{\!f}^2.$$ Two of the three angles in the ensuing triangle are given and the third can be trivially found. Then one can apply the rule of sines to get two equations and two unknowns, $v_0$ and the time of flight $t_{\!f}$.

(Edited to fix typo in the vector equation.)

 

[bremenfallturm]

In
View attachment 343380
the second term should have $v_0^2$.

Can't believe that was all there is to it - I thought I was way off! I got the formulas to work out. Thank you so much!

 

[PeroK]

Can't believe that was all there is to it - I thought I was way off! I got the formulas to work out. Thank you so much!

In projectile motion problems, the idea of looking at motion tangential to and normal to an incline doesn't make things any easier. Despite looking like a good idea. That's my opinion!

Instead, the projectile follows a parabolic path, which allows you to eliminate $t$ from the equations. Let's take the origin as the launch point and the launch angle $\theta$ above the horizontal:
$$y(t) = (v_0\sin \theta)t - \frac 1 2 gt^2, \ x(t) = (v_0\cos \theta)t$$Now, you can use$$t = \frac{x}{ v_0\cos \theta}$$to eliminate $t$ and get $y$ as a function of $x, v_0$ and $\theta$.

If you have a target at some angle $\alpha$, either above or below the horizontal, with coordinates $X, Y$, you can plug those coordinates into the equation and solve for $v_0$ or $\theta$ depending on what data you have been given. Note that in this case:
$$X = l\cos \alpha, \ Y = -l\sin\alpha$$This a good, general approach that works for lots of problems, and is worth knowing.

It's also worth knowing that$$\sec^2 \theta = 1 + \tan^2 \theta$$

 

[kuruman]

In projectile motion problems, the idea of looking at motion tangential to and normal to an incline doesn't make things any easier. Despite looking like a good idea. That's my opinion!

My opinion too. I also believe that the vector diagram shown in post #4 is, in many cases, a simplification that precludes the use of the traditional kinematic equations in component form altogether. Why break the vector equation into components if you don't have to?

 

[Hill]

Can't believe that was all there is to it - I thought I was way off! I got the formulas to work out. Thank you so much!

While @kuruman and @PeroK suggested alternative ways to approach the problem, I want to add a note which is independent of an approach.
One doesn't need to repeat the steps in order to see that the second term in the equation,

is incorrect, on dimensional grounds.
The first term on the right has dimensions of $\frac {v_0^2} g$ while the second term has dimensions of $\frac {v_0} g$; "apples and oranges" . And, while the $\frac {v_0^2} g$ has the dimension of $l$, the $\frac {v_0} g$ does not.