MHB Find Tangent Point of 2 Functions: Mikey's Calculus Help

[MarkFL]

Here is the question:

Calculus Help Please?


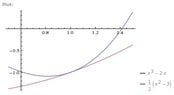
Find the point where the graphs of f(x)=x^3-2x and g(x)=0.5x^2-1.5
are tangent to each other; or have a common tangent line.

I'm pretty sure I have to find the derivatives of each and set them equal to each other. Do I then just solve for x? My answer is seems weird. Can you explain how you would go about this problem please?

Thanks.

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Mikey,

If the two given functions are tangent to each other, then the difference between the two functions will have a repeated root:

$$f(x)-g(x)=(x-a)^2(x-b)$$

$$x^3-\frac{1}{2}x^2-2x+\frac{3}{2}=x^3-(2a+b)x^2+\left(a^2+2ab \right)x-a^2b$$

Equating corresponding coefficients, we find:

$$2a+b=\frac{1}{2}$$

$$a^2+2ab=-2$$

$$a^2b=-\frac{3}{2}$$

The third equation implies:

$$b=-\frac{3}{2a^2}$$

Using this, the first equation gives:

$$4a^3-a^2-3=0\implies a=1,\,b=-\frac{3}{2}$$

And so the two functions are tangent to one another at $x=1$. Here is a plot:

View attachment 1527