Ciaran
- 71
- 0
Hi there,
I have a question I'm unable to get properly started on:
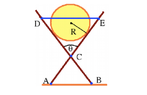
A cylinder of radius R and mass m is lodged between cross pieces that make
an angle θ with each other, as shown in the diagram below. The cross pieces
of negligible mass are connected in point C, with lengths AC = BC = 2R and
CD = CE = 3R. Determine the tension in the horizontal rope DE. You may
assume smooth floor.
Any help would be much appreciated!
View attachment 4083
I have a question I'm unable to get properly started on:
A cylinder of radius R and mass m is lodged between cross pieces that make
an angle θ with each other, as shown in the diagram below. The cross pieces
of negligible mass are connected in point C, with lengths AC = BC = 2R and
CD = CE = 3R. Determine the tension in the horizontal rope DE. You may
assume smooth floor.
Any help would be much appreciated!
View attachment 4083