Mohmmad Maaitah
- 90
- 20
- Homework Statement
- As picture
- Relevant Equations
- sum of F=ma
This is the problem and my answer below it.
my friends said it's 250 N and I say it's 100 N based on what I solved what am I missing ??

my try:
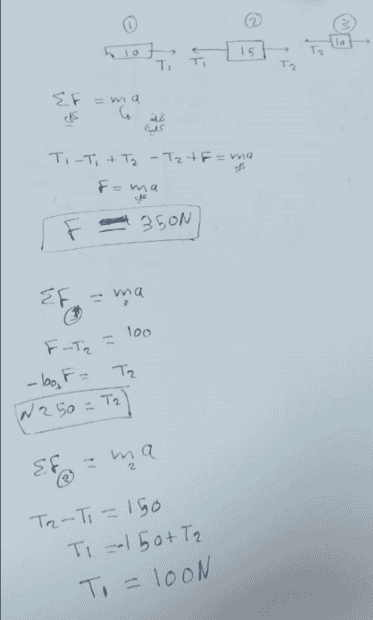
my friends said it's 250 N and I say it's 100 N based on what I solved what am I missing ??
my try: