dcmf
- 16
- 5
- Homework Statement
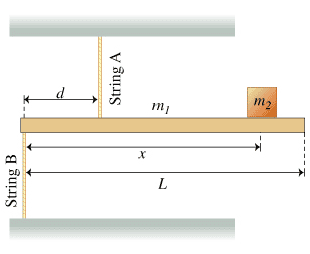
- The figure (Figure 1) shows a model of a crane that may be mounted on a truck. A rigid uniform horizontal bar of mass m1 = 90.0 kg and length L = 5.10 m is supported by two vertical massless strings. String A is attached at a distance d = 1.90 m from the left end of the bar and is connected to the top plate. String B is attached to the left end of the bar and is connected to the floor. An object of mass m2 = 2000 kg is supported by the crane at a distance x = 4.90 m from the left end of the bar. Throughout this problem, positive torque is counterclockwise and use 9.80 m/s2 for the magnitude of the acceleration due to gravity.
Find TA, the tension in string A.
- Relevant Equations
- Tnet=ΣFlsinθ, F=mg
Here's the picture of the situation described, provided by the question.
Here's a screenshot of the work I have done.
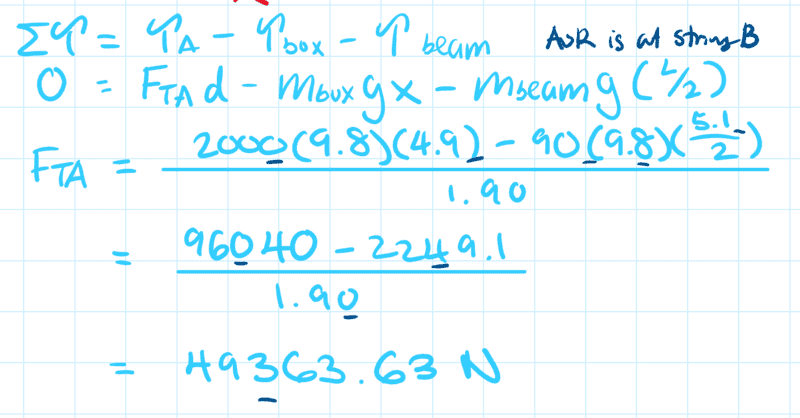
Here's a screenshot of the submission screen.
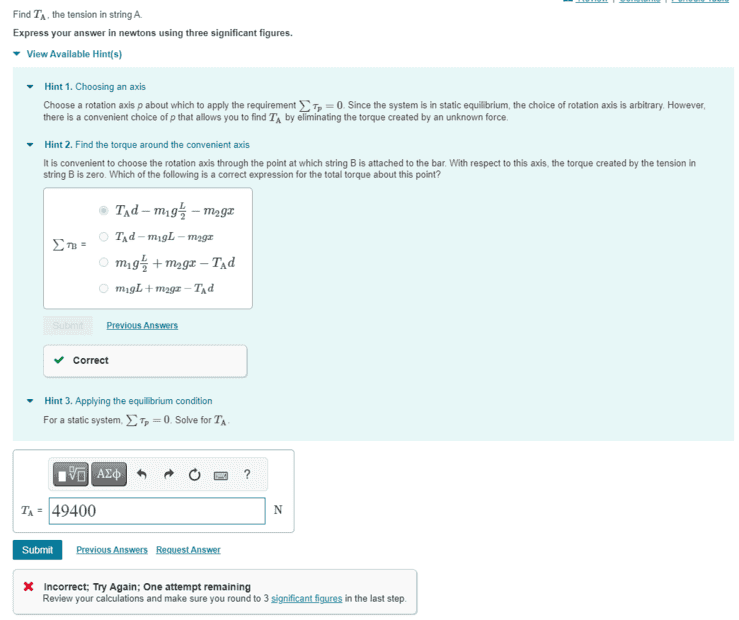
The issue is that I have one attempt left and am not sure what I am doing wrong. Based on the hints, I feel like I'm calculating it right and using the right significant figures but it's just not accepting my answer (which is strange because usually it doesn't care about significant figures). I submitted 49363.63 and was shown the incorrect message above telling me to round to 3 significant figure so I submitted 49400 and got the same message. I feel like there's got to be something really obvious I'm missing or a concept that I am not applying. I'd really appreciate the help! Thanks in advance
Here's a screenshot of the work I have done.
Here's a screenshot of the submission screen.
The issue is that I have one attempt left and am not sure what I am doing wrong. Based on the hints, I feel like I'm calculating it right and using the right significant figures but it's just not accepting my answer (which is strange because usually it doesn't care about significant figures). I submitted 49363.63 and was shown the incorrect message above telling me to round to 3 significant figure so I submitted 49400 and got the same message. I feel like there's got to be something really obvious I'm missing or a concept that I am not applying. I'd really appreciate the help! Thanks in advance