- #1
mathlearn
- 331
- 0
Hi,
View attachment 5795
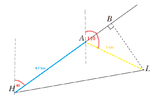
As told in the problem I drew a figure,
View attachment 5794
Next the magnitude of \(\displaystyle \angle BHL\) should be found using trigonometric tables.
Can you help me to and find the angle BHL (Smile)
Many Thanks (Smile)
View attachment 5795
As told in the problem I drew a figure,
View attachment 5794
Next the magnitude of \(\displaystyle \angle BHL\) should be found using trigonometric tables.
Can you help me to and find the angle BHL (Smile)
Many Thanks (Smile)
Attachments
Last edited: