Find the angle, cyclic quadrilaterals

[mathlearn]

View attachment 6026

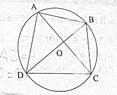
Here is a circle with center $O$

Its is given that $\angle ABD=50$ & to find the magnitudes of

$\angle ACD$ & $\angle ACB$

Now what I know is (Nerd) $\angle ACD=50$ due to the inscribed angle theorem, Can you help me to find the other angle which I don't know how to find ,stating the reasons

 

[Greg]

Do $\overline{AC}$ and $\overline{BD}$ intersect at $O$ ?

 

[mathlearn]

Do $\overline{AC}$ and $\overline{BD}$ intersect at $O$ ?

No nothing about the intersection is mentioned in the problem , But it is given that $O$ is the center of the circle

 

[Greg]

I don't think there's enough information. If $\overline{AC}$ and $\overline{BD}$ intersected at $O$ the problem wouldn't make any sense. So, are we missing anything?

 

[mathlearn]

No that is all what is given in the problem (Sadface)

 

[Greg]

Actually I goofed - - if $\overline{AC}$ intersects $\overline{BD}$ at $O$, then $\angle{ACB}=40^\circ$, so I'd assume that is the case - without that I don't think there's enough information.

 

[mathlearn]

Actually I goofed - - if $\overline{AC}$ intersects $\overline{BD}$ at $O$, then $\angle{ACB}=40^\circ$, so I'd assume that is the case - without that I don't think there's enough information.

Yes it should be :) You used "Angle at the Center Theorem" , right?

 

[Greg]

Thales' theorem. Goodnight. :)

 

[I like Serena]

Hey mathlearn! ;)

I believe it suffices if $O$ is on $BD$.
Due to Thales' theorem that implies that the required angle is 40 degrees.

Without it, we indeed do not have sufficient information.
It would mean that the angle at A does not have to be 90 degrees, implying that the required angle does not have to be 40 degrees, but could be anything. (Nerd)

Cheers!