Find the Angle of Parable Tangent from Human Running Step

[Barkiernan]

I am a masters student studying motion analysis in human running.

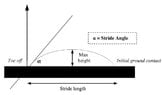
I need to find the angle of the parable tangent derived from the theoretical arc traced by a foot during a step and the ground (see attached). The arc comprises of a persons step height and step length and I need to find the angle of the arc it creates. No other research regarding this angle has manual calculated it.

I have contacted the researcher and he gave me the following formula:

Stride (step) angle tangent = 4*height / Step length
Therefore, the Stride (step) angle = tan-1(4*height/step length)”

However we are not sure why the height is multiplied by 4 ?

View attachment 9260

Thank you

 

[MarkFL]

Hello, and welcome to MHB! (Wave)

If we let \(\ell\) be the stride length, and \(h\) be the max height, and orient our coordinate axes such that the "toe off" is at the origin, then we have:

$$f(x)=kx(x-\ell)$$

Now, we must have:

$$f\left(\frac{\ell}{2}\right)=h$$

$$k\left(\frac{\ell}{2}\right)\left(\frac{\ell}{2}-\ell\right)=h\implies k=-\frac{4h}{\ell^2}$$

And so:

$$f(x)=-\frac{4h}{\ell^2}x(x-\ell)=-\frac{4h}{\ell^2}x^2+\frac{4h}{\ell}x$$

From this we find:

$$f'(x)=-\frac{8h}{\ell^2}x+\frac{4h}{\ell}$$

And then:

$$f'(0)=\frac{4h}{\ell}$$

Thus, we may conclude:

$$\alpha=\arctan\left(\frac{4h}{\ell}\right)$$