Find the angular acceleration and velocity at the end of a rod.

[MariusM]

Homework Statement

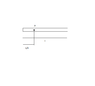
A uniform, straight rod with mass M and length L can rotate about a horizontal axis A in a distance L/4 from the rods end. Vi can disregard friction. Gravity is 9.81 m/s^2.

(drawing included at the bottom)

1) Find an expression for the moment of inertia of the rod at point A expressed by M and L.

2) The rod is initially at rest in the horizontal position shown. The rod is the released. Calculate the angular acceleration at the right end of the rod the instant it is released.

3) Calculate the angular velocity of the rod when it passes the vertical position. You can assume here that the rods length is L=1m.

Homework Equations

The first one I've already managed. I_cm+MD^2= 7ML^2/48.

The second question I would think that Ʃτ=Iα is correct.

The third I'd bring in mgy_cm=1/2*I*ω^2 (I take the Y height to be initially .5 above zero. Zero is the potential energy when it is at vertical position)

The Attempt at a Solution

2) Torque = F*r=Mg*L/3
MgL/3=7ML^2/48*α, the answer says 12.6 rad/s^2. I just can't figure out how to omit the L.

3) Using my equation stated above I get:√ (g*M*y_cm/(7/48)ML^2)=ω

I also tried using the angular velocity for both a physical pendelum (taking d to be L/3) and a simpel pendelum.

All of this is wrong. Any help would be greatly appreaciated!

 

[CrazyNinja]

All of the OP's methods are correct.

The value of L is required to get a numerical value for α and ω.

In the solution (2), the value of r should be L/2 and not L/3.