karush
Gold Member
MHB
- 3,240
- 5
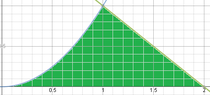
Find the area beween the curves $y=x^2$ and $x+y=2$ and the x axis
First on graphing these the $x-axis$ seem irrelevant in that it is outside the area to find.
[desmos="-10,10,-10,10"]y=x^2;y=-x+2[/desmos]
First on graphing these the $x-axis$ seem irrelevant in that it is outside the area to find.
[desmos="-10,10,-10,10"]y=x^2;y=-x+2[/desmos]