Find the area of the four sectors of the given circle

[Amer]

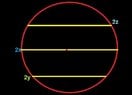
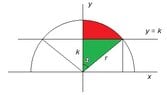
if we have the circle in the picture given x,y,z
View attachment 528

the middle line pass through the circle center
find the area of the four sectors with respect to x,y,z
parallel lines
Thanks

 

[MarkFL]

Perhaps this can get you started. Please refer to the following diagram:

View attachment 529

The area of the circular sector (the sum of the red and green areas) is:

$\displaystyle A_S = \frac{1}{2}r^2\theta$

Now, we see that:

$\displaystyle \cos(\theta)=\frac{k}{r}\,\therefore\,\theta=\cos^{-1}\left(\frac{k}{r} \right)$

and so we have:

$\displaystyle A_S = \frac{1}{2}r^2\cos^{-1}\left(\frac{k}{r} \right)$

The area of the green triangle is:

$\displaystyle A_T=\frac{1}{2}k\sqrt{r^2-k^2}$

And thus, the area A in red is:

$\displaystyle A=A_S-A_T=\frac{1}{2}\left(r^2\cos^{-1}\left(\frac{k}{r} \right)-k\sqrt{r^2-k^2} \right)$

Can you proceed from here?

 

[Amer]

Perhaps this can get you started. Please refer to the following diagram:

View attachment 529

The area of the circular sector (the sum of the red and green areas) is:

$\displaystyle A_S = \frac{1}{2}r^2\theta$

Now, we see that:

$\displaystyle \cos(\theta)=\frac{k}{r}\,\therefore\,\theta=\cos^{-1}\left(\frac{k}{r} \right)$

and so we have:

$\displaystyle A_S = \frac{1}{2}r^2\cos^{-1}\left(\frac{k}{r} \right)$

The area of the green triangle is:

$\displaystyle A_T=\frac{1}{2}k\sqrt{r^2-k^2}$

And thus, the area A in red is:

$\displaystyle A=A_S-A_T=\frac{1}{2}\left(r^2\cos^{-1}\left(\frac{k}{r} \right)-k\sqrt{r^2-k^2} \right)$

Can you proceed from here?

Thanks I can for sure, we have the semicircle area
the quarter area of the circle minus the area of the red we will get the semi area of below sector.