chwala
Gold Member
- 2,827
- 415
- Homework Statement
- See attached
- Relevant Equations
- Circular measure
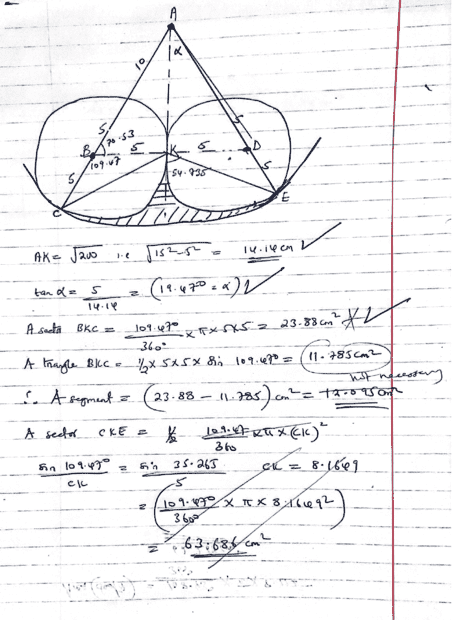
Wawawawawa boggled me a little bit... but finally managed it...seeking alternative approach guys;
kindly note that what i have indicated as ##*## and a ##√## is the correct working ...
Text book answer indicates ##17.5## as answer... will re check my rounding solutions later...

My working- allow me to copy paste here...will later type the working...
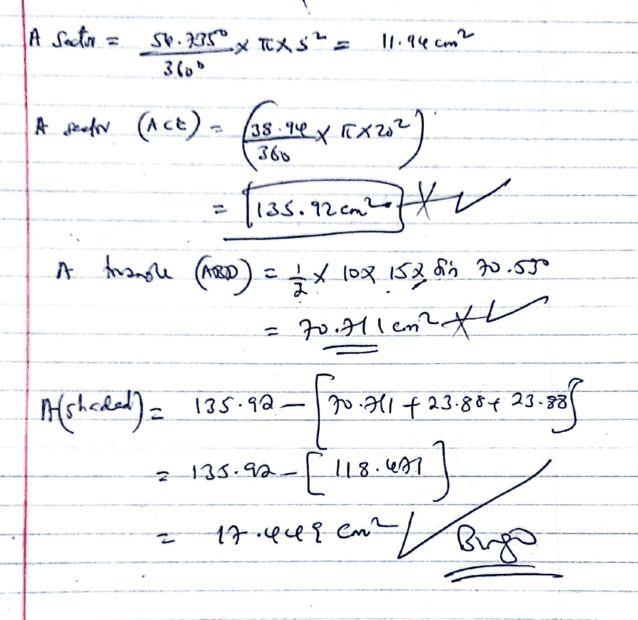
kindly note that what i have indicated as ##*## and a ##√## is the correct working ...
Text book answer indicates ##17.5## as answer... will re check my rounding solutions later...
My working- allow me to copy paste here...will later type the working...
Last edited: