Find the Bearing from A to C & Angle B: Solve Here

[cbarker1]

Dear everyone,

An airplane flies 470 miles from point $A$ to point $B$ with a bearing of 25 degrees. It then flies from 250 miles from point $B$ to point $C$ with a bearing of 40 degrees. Find the distance and the bearing from A to point C.
Work

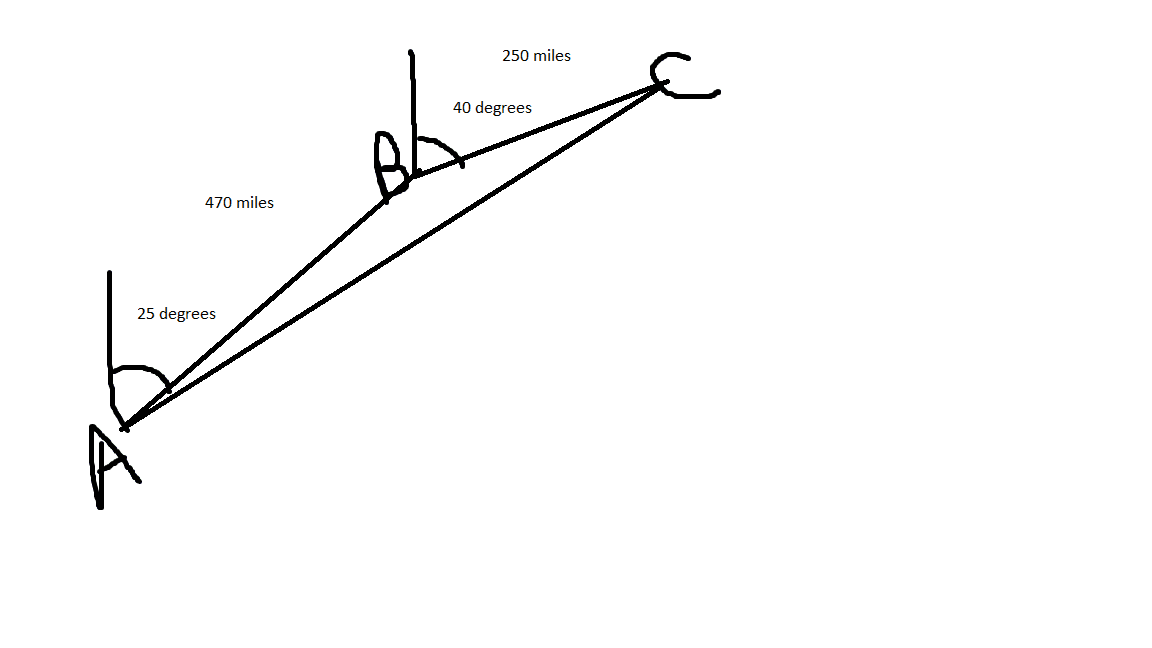
I understand that I need to use law of cosines for the side $b$ which is opposite of the angle $B$. But I have a hard time with find what is the angle $B$ is. I forgot many things from geometry. How to determine the angle from point $A$ to point $C$?

Thanks
Cbarker1

 

[skeeter]

$AC = \sqrt{470^2+250^2 - 2(470)(250)\cos(165)}$

bearing = $25^\circ + m\angle{BAC}$

$\angle{BAC}$ may be found using either the sine or cosine law

 

[cbarker1]

How did you determine the angle ABC to be 165?

 

[skeeter]