Find the Cartesian equation of a curve given the parametric equation

[chwala]

Homework Statement

Kindly see attached below

Relevant Equations

parametric equations

My interest on this question is solely on $10.iii$ only... i shared the whole question so as to give some background information.

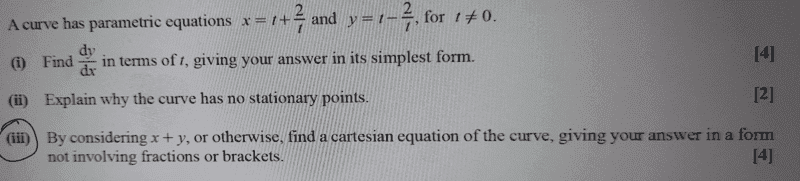
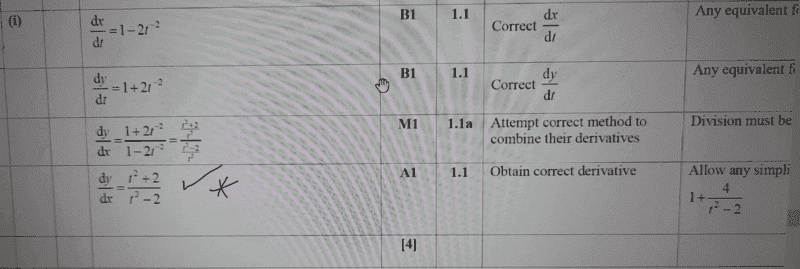
the solution to $10.iii$ here,

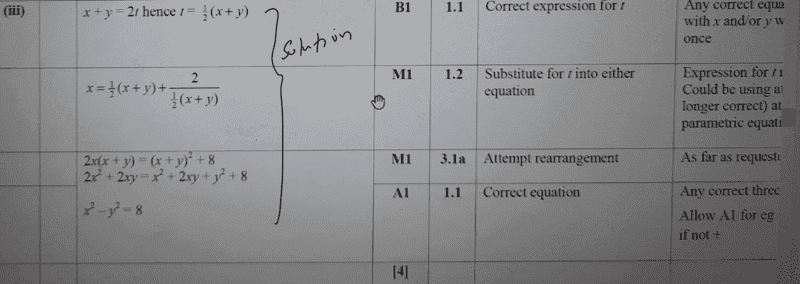
now my question is, what if one would approach the question like this,
$\frac {dy}{dx}=\frac{t^2+2}{t^2-2}$
we know that $xt=t^2+2$
$yt=t^2-2$,
therefore, $\frac {dy}{dx}=\frac{x}{y}$
it follows that, $ydy=xdx$ on integration, $\frac {y^2}{2}+k=\frac {x^2}{2}$, or
$x^2-y^2=2k$, would this be correct? (...if a student was to answer using this approach in an exam i.e...)
I know that the $k$ value here is not assigned the required numeric value $8$...

 

[Delta2]

Yes it would be correct. But you would have to find a way to find k, probably using the fact that $$x^2-y^2=(t+\frac{2}{t})^2-(t-\frac{2}{t})^2=...=8$$

 

[chwala]

Yes it would be correct. But you would have to find a way to find k, probably using the fact that $$x^2-y^2=(t+\frac{2}{t})^2-(t-\frac{2}{t})^2=...=8$$

which takes us back to the mark scheme method...going round in a circle...would the student get full marks for my approach or will he miss a mark for not having the $k$ value?

 

[Delta2]

which takes us back to the mark scheme method...going round in a circle...would the student get full marks for my approach or will he miss a mark for not having the $k$ value?

I think he will miss some points for not having the $k$ value...something like 10%-25% of the total points.

 

[chwala]

Thanks delta... its a $4$ mark question, my quick guess is that a student would score $3$ marks...cheers mate.

 

[kuruman]

If one has already seen that adding the two equations drops the reciprocal $t$ terms, then it should be obvious that subtracting the equations drops the $t$ terms:
$x+y=2t$
$x-y=\dfrac{4}{t}$
Multiplying the equations drops the $t$ dependence on the right
$(x+y)(x-y)=8.$

 

[chwala]

If one has already seen that adding the two equations drops the reciprocal $t$ terms, then it should be obvious that subtracting the equations drops the $t$ terms:
$x+y=2t$
$x-y=\dfrac{4}{t}$
Multiplying the equations drops the $t$ dependence on the right
$(x+y)(x-y)=8.$

nice kuruman,...looks like i can use your approach in solving simultaneous equations in the future...i did not realize one can multiply the expressions the way you've done. Brilliant mate!