Find the center of gravity of a combined cone and cylinder

[gnits]

Homework Statement

Find center of gravity of combined cone and cylinder

Relevant Equations

Moments

Could I please ask for help with the following:

Given: The centre of gravity of a uniform solid right circular cone of vertical height h and base radius a is at a distance 3h/4 from the vertex of the cone.

Such a cone is joined to a uniform solid right circular cylinder of the same material and of height h and base radius a, so that the plane base of the cone coincides with a plane face of the cylinder. Find the distance of the centre of gravity of the solid from the centre of the base of the cone.

I've done this, the answer is 5h/16

When the cone hangs in equilibrium from a point A on the circumference of the base of the cone, the line joining A to the vertex of the cone is horizontal, Prove that 4a = sqrt(5)*h

This is the part I need help with. Here's a diagram:

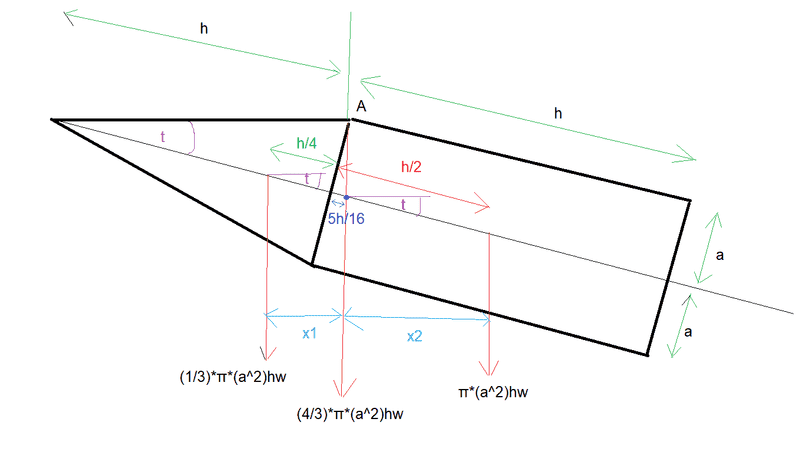
So I reasoned that the moment about A should be zero.

I let the half-angle of the cone be t.

Then I get:

x1 = 9hcos(t)/16
x2 = 3hcos(t)/16

Taking moments about A I get:

πa^2hw * 3hcos(t)/16 = (1/3)πa^2hw * 9hcos(t)/16

Which is gives 1 = 1.

Thanks for any help,
Mitch.

 

[haruspex]

It all cancels because your equation merely confirms that the common mass centre is where you calculated it to be.
You have not actually used that the top edge of the cone is horizontal.

 

[Delta2]

You have not actually used that the top edge of the cone is horizontal.

I also wonder how we can actually use this fact and translate it into an equation. If it is not used when we take the moments equation then in what equation it can be used?
Is this some sort of purely geometrical solution, where the only thing we take from physics is that some lines will be horizontal or vertical and some angles will be 90 degrees?

 

[Steve4Physics]

I also wonder how we can actually use this fact and translate it into an equation. If it is not used when we take the moments equation then in what equation it can be used?
Is this some sort of purely geometrical solution, where the only thing we take from physics is that some lines will be horizontal or vertical and some angles will be 90 degrees?

Yes, it's a purely geometrical exercise. The overall centre of gravity must lie vertically below A.

Therefore there must be a relationship between a and h which makes the line joining A to the vertex of the cone exactly horizontal (as opposed to some arbitrary angle).

 

[gnits]

I also wonder how we can actually use this fact and translate it into an equation. If it is not used when we take the moments equation then in what equation it can be used?
Is this some sort of purely geometrical solution, where the only thing we take from physics is that some lines will be horizontal or vertical and some angles will be 90 degrees?

I see now that indeed all of the equations I had derived are true regardless of the orientation of the object and so always true, hence 1 = 1,

So somehow I need to use the extra condition\constraint that VA is horizontal (where V is the vertex of the cone). Well, that tells me that the angle VAM = 90 (Where M = centre of mass of the object).

Still looking …

 

[gnits]

Could I please ask for a pointer in the right direction?

Here's a less cluttered diagram:

So it's a purely geometrical argument we need. Which relationship between a and h will yield VA horizontal.

In going from A to G that's a distance of (using Pythagoras) of sqrt( a^2 + (5h/16)^2 ).

So we could equate this to the vertical distance traveled in moving from G to V, which is (21h/16)*sin(t) (because horizontal VA means that angle VAG = 90)

So we need to replace sin(t) with something in terms of a and h. Well we know that tan(t)=5h/16a. Can use 1 + cot^2 = cosec^2 to get expression for sin(t) in terms of a and h.

Am I missing a simpler way?

Thanks,
Mitch.

 

[Steve4Physics]

Am I missing a simpler way?

This is may be too much help, but since it just looks like you've hit a simple blind spot...

Let P be the centre of the cone's base. Triangles AVP and AGP are similar. (They don't look it on your diagram, but that's because your diagram is not accurately to scale.)

What do you know about the ratios of sides in similar triangles? (Alternatively write down an expression for tan(t) in each triangle.) The required answer then comes out in a few (simple) lines.

Edit: minor wording change

 

[gnits]

This is may be too much help, but since it just looks like you've hit a simple blind spot...

Let P be the centre of the cone's base. Triangles AVP and AGP are similar. (They don't look it on your diagram, but that's because your diagram is not accurately to scale.)

What do you know about the ratios of sides in similar triangles? (Alternatively write down an expression for tan(t) in each triangle.) The required answer then comes out in a few (simple) lines.

Edit: minor wording change

Thank you very much, "blind spot" is the right term for it. I just didn't see it. Tried all sorts. Thank you again.