Argonaut
- 45
- 24
- Homework Statement
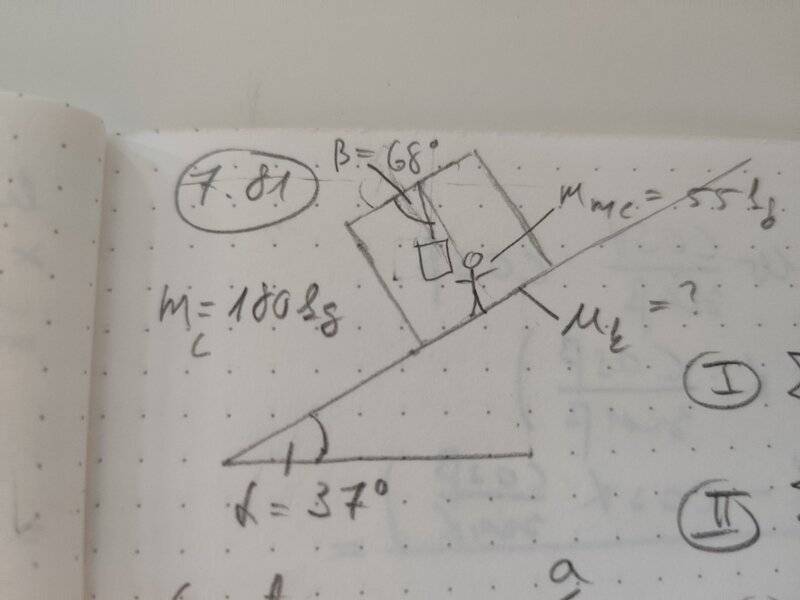
- A steel washer is suspended inside an empty shipping crate from a light string attached to the top of the crate. The crate slides down a long ramp that is inclined at an angle of 37° above the horizontal. The crate has mass 180 kg. You are sitting inside the crate(with a flashlight); your mass is 55 kg. As the crate is sliding down the ramp, you find the washer is at rest with respect to the crate when the string makes an angle of 68° with the top of the crate. What is the coefficient of kinetic friction between the ramp and the crate?
- Relevant Equations
- Newton's First and Second Laws
Young & Freedman 13th ed, Exercise 7.81
Starting with the crate, here is its free-body diagram:
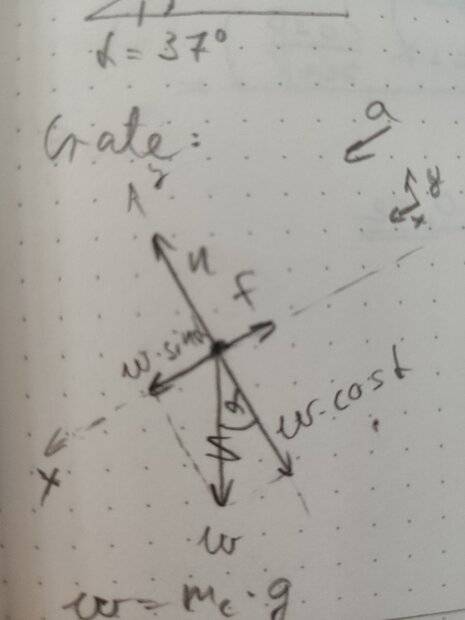
In accordance with Newton's First Law:
$$ \Sigma F_y = 0 = n+(-w_c \cos{\alpha}) $$
Thus ## n = w_c \cos{\alpha} ##.
And according to Newton's Second Law:
$$ \Sigma F_x = m_c a_x = w_c \sin{\alpha} + (-f) $$
Utilising the fact that ## f = \mu_k n ## and substituting n with the expression above, we get:
$$
\begin{align*}
m_c a_x &= w_c \sin{\alpha} - \mu_k n \\
&= w_c \sin{\alpha} - \mu_k w_c \cos{\alpha} \\
&= m_c g (\sin{\alpha} - \mu_k \cos{\alpha})
\end{align*}
$$
Thus ## \mu_k = \frac{\sin{\alpha} - a_x/g}{\cos{\alpha}} ##.
##a_x## is unknown. Switching to the washer, it's free-body diagram:
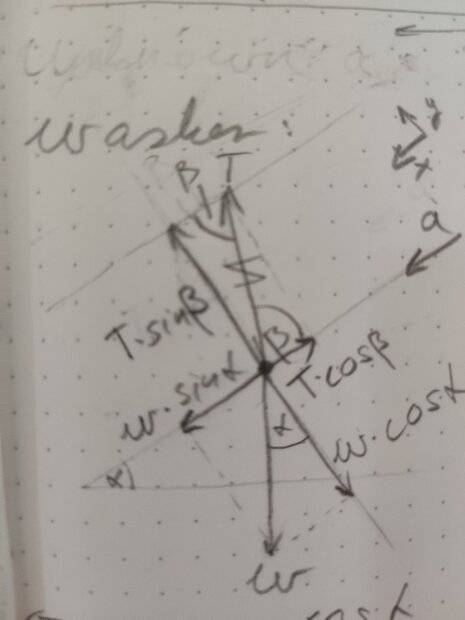
According to Newton's First Law:
$$ \Sigma F_y = 0 = T \sin{\beta} - w_w \cos{\alpha} $$
Thus we have ## T = w_w \frac{\cos{\alpha}}{\sin{\beta}} ##.
According to Newton's Second Law:
$$ \Sigma F_x = m_w a_x = w_w \sin{\alpha} -T \cos{\beta} $$
Substituting T with the expression above and rearranging to express ## a_x ##, we get:
$$
\begin{align*}
m_w a_x &= w_w \sin{\alpha} -T \cos{\beta} \\
&= w_w \sin{\alpha} - w_w \frac{\cos{\alpha}}{\sin{\beta}} \cos{\beta}
\end{align*}
$$
Thus ## a_x = g( \sin{\alpha} - \frac{\cos{\alpha}}{\sin{\beta}} \cos{\beta}) ##
Plugging in ##a_x##to the expression for ## \mu_k##, we get:
$$
\begin{align*}
\mu_k &= \sin{\alpha}( \sin{\alpha} - \frac{\cos{\alpha}}{\sin{\beta}} \cos{\beta})/\cos{\alpha} \\
&= \frac{\cos{\beta}}{\sin{\alpha}} \\
&= \frac{\cos{68°}}{\sin{37°}} \\
&\approx 0.62
\end{align*}
$$
The book solution says it's 0.40. Where did I make a mistake?
Starting with the crate, here is its free-body diagram:
In accordance with Newton's First Law:
$$ \Sigma F_y = 0 = n+(-w_c \cos{\alpha}) $$
Thus ## n = w_c \cos{\alpha} ##.
And according to Newton's Second Law:
$$ \Sigma F_x = m_c a_x = w_c \sin{\alpha} + (-f) $$
Utilising the fact that ## f = \mu_k n ## and substituting n with the expression above, we get:
$$
\begin{align*}
m_c a_x &= w_c \sin{\alpha} - \mu_k n \\
&= w_c \sin{\alpha} - \mu_k w_c \cos{\alpha} \\
&= m_c g (\sin{\alpha} - \mu_k \cos{\alpha})
\end{align*}
$$
Thus ## \mu_k = \frac{\sin{\alpha} - a_x/g}{\cos{\alpha}} ##.
##a_x## is unknown. Switching to the washer, it's free-body diagram:
According to Newton's First Law:
$$ \Sigma F_y = 0 = T \sin{\beta} - w_w \cos{\alpha} $$
Thus we have ## T = w_w \frac{\cos{\alpha}}{\sin{\beta}} ##.
According to Newton's Second Law:
$$ \Sigma F_x = m_w a_x = w_w \sin{\alpha} -T \cos{\beta} $$
Substituting T with the expression above and rearranging to express ## a_x ##, we get:
$$
\begin{align*}
m_w a_x &= w_w \sin{\alpha} -T \cos{\beta} \\
&= w_w \sin{\alpha} - w_w \frac{\cos{\alpha}}{\sin{\beta}} \cos{\beta}
\end{align*}
$$
Thus ## a_x = g( \sin{\alpha} - \frac{\cos{\alpha}}{\sin{\beta}} \cos{\beta}) ##
Plugging in ##a_x##to the expression for ## \mu_k##, we get:
$$
\begin{align*}
\mu_k &= \sin{\alpha}( \sin{\alpha} - \frac{\cos{\alpha}}{\sin{\beta}} \cos{\beta})/\cos{\alpha} \\
&= \frac{\cos{\beta}}{\sin{\alpha}} \\
&= \frac{\cos{68°}}{\sin{37°}} \\
&\approx 0.62
\end{align*}
$$
The book solution says it's 0.40. Where did I make a mistake?
