- #1
msrultons
- 3
- 1
- Homework Statement
- use the fundamental theorem of calculus to find the derivative of y= u^5/(1+u^3) from 8 to 8-7x
- Relevant Equations
- Fundamental Theorem of Calculus
Here is the problem
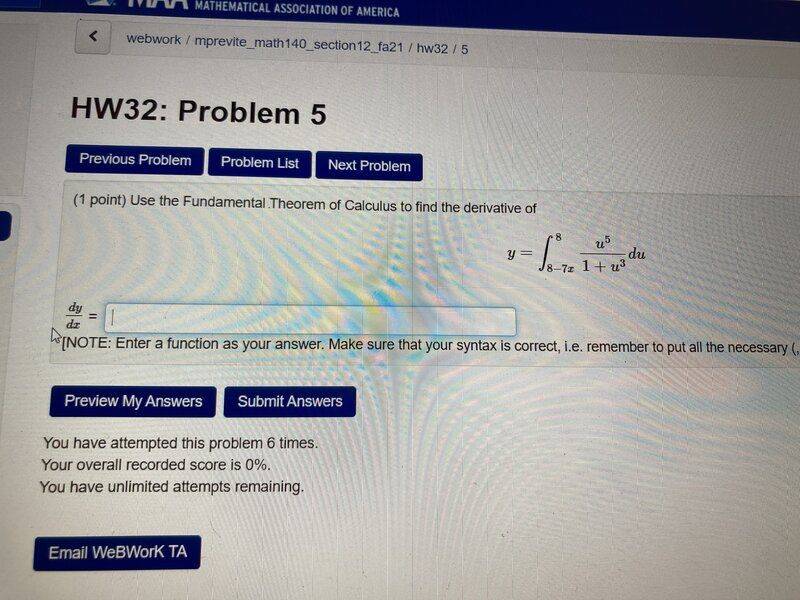
Here is my work on it. I thought I did it correct, but again, was told it was wrong.
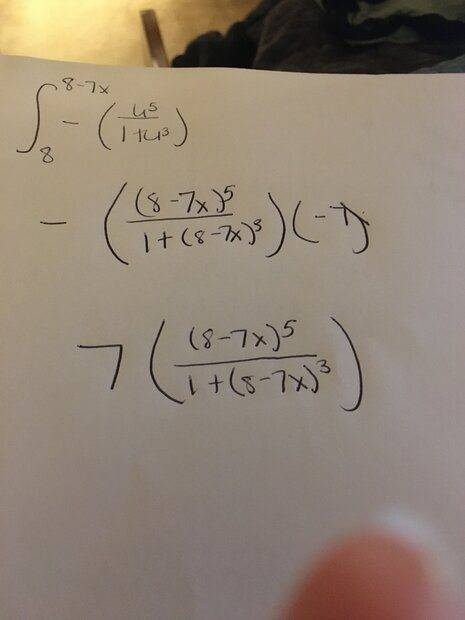
Here is my work on it. I thought I did it correct, but again, was told it was wrong.