chwala
Gold Member
- 2,827
- 415
- Homework Statement
- Kindly see attached problem
- Relevant Equations
- domain and inverse of functions concept
This is a textbook problem:

now for part a) no issue here, the range of the function is ##-1≤f(x)≤299##
now for part b)
i got ##x≥-1##
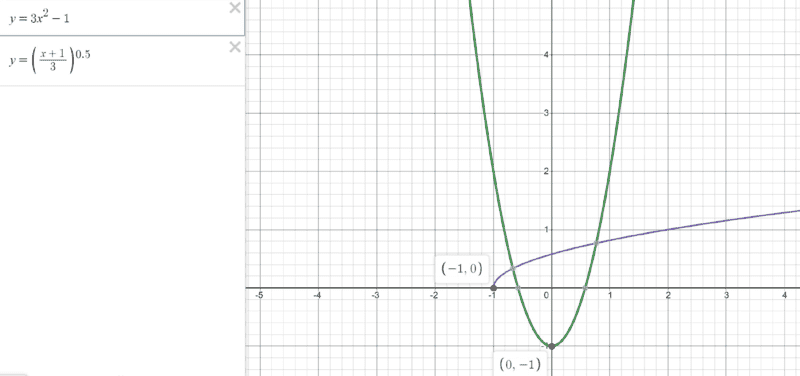 but the textbook indicates the solution as ##x≥0## hmmmmm i think, that's not correct...
but the textbook indicates the solution as ##x≥0## hmmmmm i think, that's not correct...
now for part a) no issue here, the range of the function is ##-1≤f(x)≤299##
now for part b)
i got ##x≥-1##