chwala
Gold Member
- 2,827
- 415
- Homework Statement
- See attached textbook question and solution
- Relevant Equations
- Integration - Calculus
This is the question...hmmmm it stressed me a little bit.
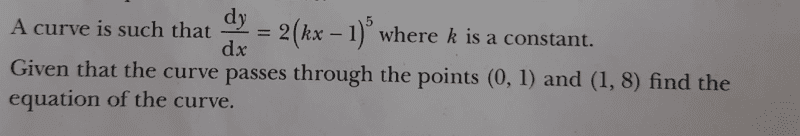
Find the textbook solution here; no. 6
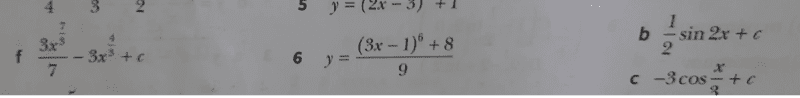
Now my approach to this was as follows;
On integration,
##y=\dfrac{(kx-1)^6}{3k} +c##
on using the point ##(0,1)## and ##(1,8)##, we end up with
##1=\dfrac{1}{3k} +c##
##8=\dfrac{(k-1)^6}{3k} +c##
it follows that,
##8=\dfrac{(k-1)^6}{3k} + \dfrac{3k-1}{3k} ##
...
##(k-1)^6+3k-1-24k=0##
##(k-1)^6-21k-1=0##
##k^6-6k^5+15k^4-20k^3+15k^2-6k+1-21k-1=0##
I let ##P(k)=k^6-6k^5+15k^4-20k^3+15k^2-6k+1-21k-1##
using trial and error method from ##±0, ±1...## i got ##P(3)=0## implying ##k=3## is a factor,
thus substituting on;
##1=\dfrac{1}{3k} +c##
we get;
##1=\dfrac{1}{3×3} +c##
##1=\dfrac{1}{9} +c##
##c=\dfrac{8}{9}##
Therefore;
##y=\dfrac{(3x-1)^6}{3×3} +\dfrac{8}{9}##
##y=\dfrac{(3x-1)^6+8}{9}##
I would be interested if there would be another approach to this question. Cheers guys.
Find the textbook solution here; no. 6
Now my approach to this was as follows;
On integration,
##y=\dfrac{(kx-1)^6}{3k} +c##
on using the point ##(0,1)## and ##(1,8)##, we end up with
##1=\dfrac{1}{3k} +c##
##8=\dfrac{(k-1)^6}{3k} +c##
it follows that,
##8=\dfrac{(k-1)^6}{3k} + \dfrac{3k-1}{3k} ##
...
##(k-1)^6+3k-1-24k=0##
##(k-1)^6-21k-1=0##
##k^6-6k^5+15k^4-20k^3+15k^2-6k+1-21k-1=0##
I let ##P(k)=k^6-6k^5+15k^4-20k^3+15k^2-6k+1-21k-1##
using trial and error method from ##±0, ±1...## i got ##P(3)=0## implying ##k=3## is a factor,
thus substituting on;
##1=\dfrac{1}{3k} +c##
we get;
##1=\dfrac{1}{3×3} +c##
##1=\dfrac{1}{9} +c##
##c=\dfrac{8}{9}##
Therefore;
##y=\dfrac{(3x-1)^6}{3×3} +\dfrac{8}{9}##
##y=\dfrac{(3x-1)^6+8}{9}##
I would be interested if there would be another approach to this question. Cheers guys.
Last edited: