- #1
zenterix
- 758
- 84
- Homework Statement
- Find the equivalent resistance of this circuit (Problem 2.3 of Chapter 2 of Agarwal's Foundations of Analog and Digital Electronic Circuits.
- Relevant Equations
- I will use symmetry.
Consider the following circuit where all resistors have resistance ##1 \Omega##.
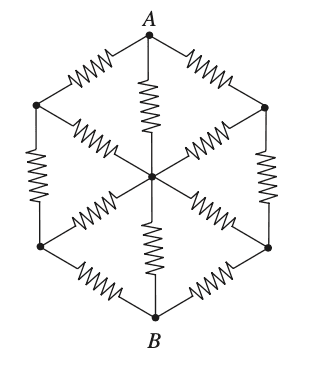
We would like to find the equivalent resistance.
My solution differs from the answer at the end of the book I am reading, so I would like to know what I did wrong, or if the book is wrong.
Here is what I did
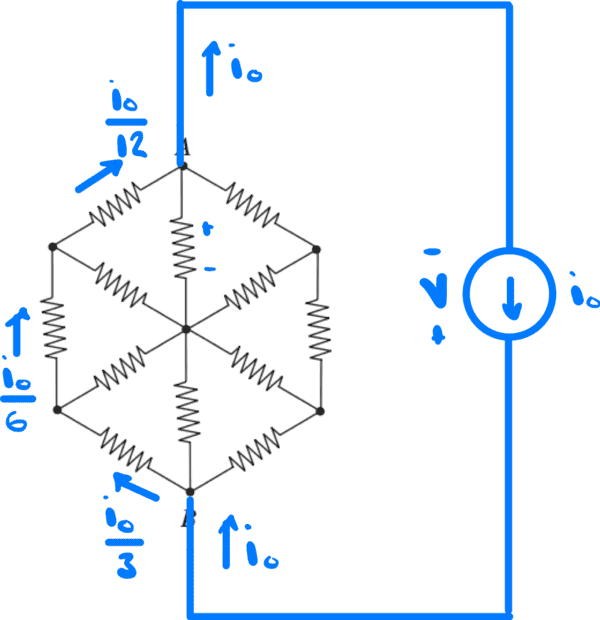
I used symmetry to determine the currents on the resistors.
Then I used KVL on the loop that includes these outer resistors and passing through the current source, assuming that the potential difference between a point below the current source (+) and a point above it (-) is V.
##\frac{i_0}{3}+\frac{i_0}{6}+\frac{i_0}{12}-V=0##
##V=\frac{7i_0}{12}=i_0R_{eq}##
##R_{eq}=\frac{7}{12}\Omega##
This seems right to me, but the book says the answer is ##\frac{4}{5}\Omega##
What am I missing?
We would like to find the equivalent resistance.
My solution differs from the answer at the end of the book I am reading, so I would like to know what I did wrong, or if the book is wrong.
Here is what I did
I used symmetry to determine the currents on the resistors.
Then I used KVL on the loop that includes these outer resistors and passing through the current source, assuming that the potential difference between a point below the current source (+) and a point above it (-) is V.
##\frac{i_0}{3}+\frac{i_0}{6}+\frac{i_0}{12}-V=0##
##V=\frac{7i_0}{12}=i_0R_{eq}##
##R_{eq}=\frac{7}{12}\Omega##
This seems right to me, but the book says the answer is ##\frac{4}{5}\Omega##
What am I missing?