Find the force and the torque so that the cylinder is in balance

[mathmari]

Hey!

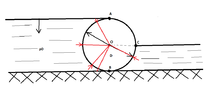
At the cylinder of the picture there are static pressures from environment fluid of density $\rho$. If we neglect the atmospheric pressure, calculate how much force and how much torque is needed so that the cylinder balance.

View attachment 4436

In my notes there is the solution, but I haven't really understood it...

The Euler equation is $$\rho \frac{D \overrightarrow{u}}{D T}=-\nabla p+\rho \overrightarrow{b}$$

Since the cylinder should be in balance we have that $\overrightarrow{u}=0$.

We also have that $\overrightarrow{b}=\overrightarrow{g}$

That means that $$\nabla p=\rho \overrightarrow{b}=\rho \overrightarrow{g}$$

Since $\overrightarrow{g}=-g\hat{k}$ we have that $$\nabla p=-\rho_0 g \hat{k} \Rightarrow \partial_xp=0 \ \ , \ \ \partial_yp=0 \ \ , \ \ \partial_zp=-\rho_0 g$$

$$\Rightarrow \frac{dp}{dz}=-\rho_0 g \Rightarrow p(z)=-\rho_0 g z+\lambda$$

Is it correct so far?? (Wondering) After that in my notes there is the following which I don't understand:

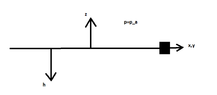
$$p(z)=-\rho_0 g z+\lambda$$

View attachment 4437

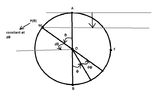
$$z=0 \ \ \ \ \ p(z=0)=\lambda =p_a \\ p(z)-p_a=-\rho g z=-\rho_0 g h$$

View attachment 4438

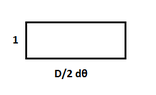
$$P(\theta)=\rho_0 g h(\theta)=\rho_0 g\frac{D}{2}(1-\cos \theta)$$

$$P(\theta) dA=P(\theta)\left (1 \cdot \frac{D}{2}d\theta\right )$$

View attachment 4439

$$F_{AB}=\int_{\theta=0}^{\theta=\pi} p(\theta)\frac{D}{2}d \theta \\ F_{B \Gamma}= \dots $$

Could you explain to me the part I don't understand?? (Wondering)

 

[mathmari]

I have the following questions:

Why is for $z=0$, $p=p_a$ ?? And also why do we replace $z$ with $h$ ??

At the end to compute the force do we take the integral to add the force at each part at which we divide the cylinder??

Since $\theta$ is the angle from $A$ and we want to calculate the force from A to B we take the limits $\theta=0$ to $\theta=\pi$, right?? So, to find the force $F_{B \Gamma}$ we have to calculate the integral $\int_{\phi=0}^{\phi=\frac{\pi}{2}} p(\phi)\frac{D}{2}d \phi$, right??

Which is the force and which is the torque that we are looking for at the solution of my notes??

(Wondering)