Find the height to which a mass rises

[gnits]

Homework Statement

To find the height to which a mass rises

Relevant Equations

PE=mgh

Hi,

Could I please ask for help regarding the following question.

The book answer H = ( 3 - 3 sqrt(2)/4 ) L

(natural length of string is L)

Here is my diagram:

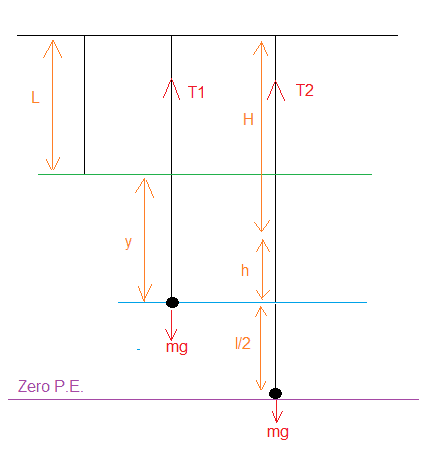
The green level represents the unstretched string.
The blue level is the string and mass in equilibrium.
The purple level is the mass at its lowest level.

When the mass reaches the blue level it will pick up the rider.

Here's my method:

Equating forces in the equilibrium positions gives: (using tension in elastic string = Yx/L where Y = elastic modulus, x = extension and L = natural length.)

mgy/L = mg

and so we find that y = L. This is the equilibrium position of the sphere.

I am solving the problem by considering energy. Energy in elastic string = Yx^2/ 2L

Let h be the maximum height above the equilibrium position which the combined masses reach.

So, equating energy at lowest point (all elastic energy) to energy at highest point to which sphere and rider rise (remaining elastic energy plus potential energy of the mass of the sphere and rider) gives:

( mg(L + L/2)^2 ) / ( 2L ) = ( mg(L - h)^2) / ( 2L ) + ( 2mg( (L/2) + h ) )

This doesn't lead me to the books answer.

Is this a valid way to attack the problem? If so, what silly mistake have I made?

Thanks for any help,
Mitch.

 

[haruspex]

equating energy at lowest point (all elastic energy) to energy at highest point to which sphere and rider rise

Never assume without good reason that mechanical energy is conserved.
What do you know in that regard about the process by which the sphere collects the rider?

 

[gnits]

Thanks for you clue. Indeed I was wrong to assume conservation of mechanical energy in the inelastic collision. Here is my now correct approach. I can show that the initial motion before the collision is SHM of amplitude L/2 about the blue level. I can use this to give me the velocity of the sphere just before the impact. This comes out to v1 = (1/2)sqrt(g/L). Now the masses collide. I use conservation of momentum to give me the velocity of the combined masses and this gives v2 = (1/4)sqrt(g/L). Now I equate the energy in the system at this instant just after the collision with that in the system once the combined mass reaches the highest point of its motion (a distance h above the blue level)

I define zero potential energy as being at the blue level. so:

Elastic energy in string at blue level + K.E. of combined mass = Elastic energy in string at h above blue level + P.E. of combined mass. This gives:

mgL^2/2L + (1/2)*2M*gL/16 = mg(L-h)^2/2L + 2mgh

Solving this for h and gives the correct answer of 2L - h.

Thanks very much.

 

[haruspex]

Thank you for taking the trouble to post your corrected answer.