Find the indefinite integral of the given problem

[chwala]

Homework Statement

see attached

Relevant Equations

$\dfrac{d}{dx} \left[\tan^{-1}x\right]= \dfrac{1}{x^2+1}$

Now the steps to solution are clear to me...My interest is on the constant that was factored out i.e $\frac{2}{\sqrt 3}$...

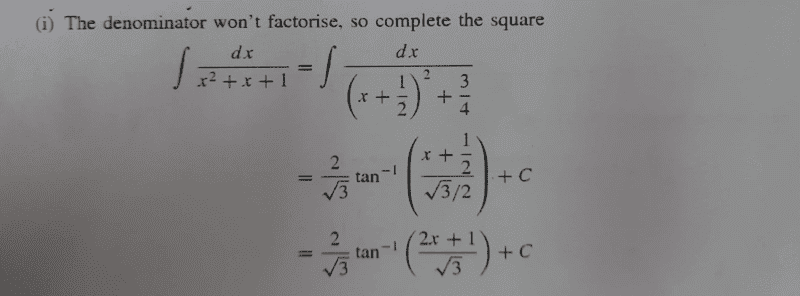the steps that were followed are; They multiplied each term by $\dfrac{2}{\sqrt 3}$ to realize,

$\dfrac{2}{\sqrt 3}\int \dfrac{dx}{\left[\dfrac{2}{\sqrt 3}⋅\dfrac{2x+1}{2}\right]^2+\left[\dfrac{2}{\sqrt 3}⋅\dfrac{\sqrt 3}{2}\right]^2}$

...

Correct? Is there a different approach guys?

Now, bringing me to my question...see problem below;

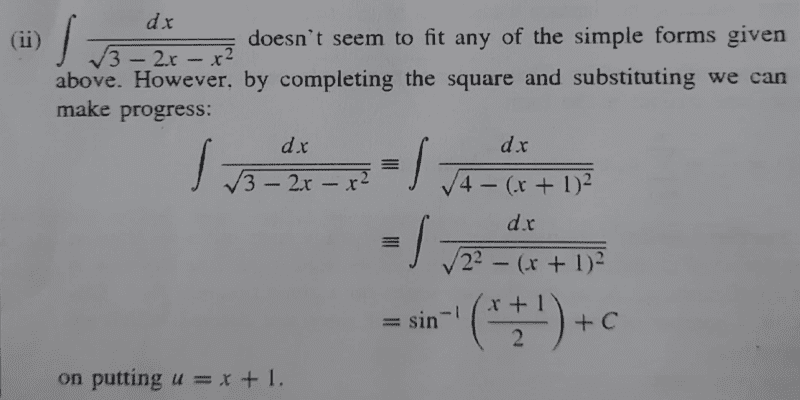
Are they missing $\dfrac{1}{2}$ somewhere?? In this case we are dividing each term by $2^2$... we ought to have;

... $\dfrac{1}{2}\sin^{-1} \left[\frac{x+1}{2}\right] + c$

I hope i did not overlook anything...

 

[pasmith]

$$\int \frac{1}{\sqrt{2^2 - (x + 1)^2}}\,dx = \int \frac{1}{2\sqrt{1 - u^2}}(2\,du)$$ with $u = (x + 1)/2$.

 

[chwala]

$$\int \frac{1}{\sqrt{2^2 - (x + 1)^2}}\,dx = \int \frac{1}{2\sqrt{1 - u^2}}(2\,du)$$ with $u = (x + 1)/2$.

Thanks ...cheers man!

 

[chwala]

Aaaargh! because of the square root sign! That calls for 'change of variable' ...was wondering why...great day!