Find the inequality that satisfies this quadratic problem

[chwala]

Homework Statement

see attached...

Relevant Equations

quadratic equations...

see the textbook problem below;

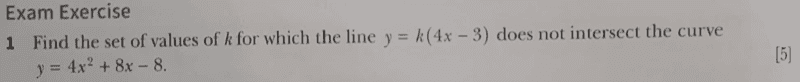see my working to solution below;

i generally examine the neighbourhood of the critical values in trying to determine the correct inequality. My question is
"is there a different approach other than checking the neighbourhood of the critical values"? In other words, i am seeking an alternative approach.

cheers guys...

 

[fresh_42]

I got the same result, but I used the same method. The quadratic equation for $k$ is $k^2-7k+12<0$. This is a parabola, opened at the top, so all values between the two zeros have to be negative, and the zeros are $7/2\pm \sqrt{1/4}.$

What other method do you mean? Without the parabola in mind, we can write
$$
k^2-7k+12=(k-4)\cdot(k-3) < 0
$$
In order for a product to be negative, the two factors must be of different signs. So we have the options $k-4>0$ and $k-3<0$ which is impossible, or $k-4<0$ and $k-3>0$ which is the solution.

 

[chwala]

I meant another approach...cheers Fresh ...cheers mate, i find it much easier just to examine the neighbourhood of the critical values $k$ and i check whether they satisfy the given inequality...this is similar to your analysis that you have shown on your last paragraph. Cheers.

 

[fresh_42]

I meant another approach...cheers Fresh ...cheers mate, i find it much easier just to examine the neighbourhood...its pretty straightforward.

Yes. Once you know the zeros of the equation you are done, one way or the other. I scribbled the parabola and "saw" that we are looking for the in-betweens. I only added the consideration with the factors as an additional way to get the result.

The direct investigation of the straights $y=k(4x-3)$ is a bit difficult because $k$ changes slope and the point where the straight crosses a coordinate axis simultaneously. I see no way to get a hold of this line bundle. Calculating the intersection points is easier.