chwala
Gold Member
- 2,827
- 415
- Homework Statement
- see attached
- Relevant Equations
- Integration
This question is from a Further Maths paper;
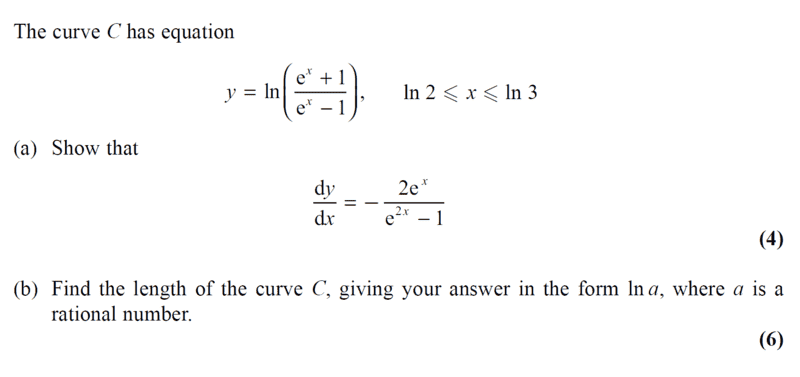
Part (a) is pretty straight forward...No issue here...one has to use chain rule...
Let ##U=\dfrac{e^x+1}{e^x-1}## to realize ##\dfrac{du}{dx}=\dfrac{-2e^x}{(e^x-1)^2}##
and let
##y=\ln u## on taking derivatives, we shall have ##\dfrac{dy}{du}=\dfrac{e^x-1}{e^x+1}##
therefore,
##\dfrac{dy}{dx}=\dfrac{e^x-1}{e^x+1}×\dfrac{-2e^x}{(e^x-1)^2}=-\dfrac{2e^x}{(e^{2x}-1)^2}##Now my question (reason for posting this problem is on part b). Why do we have ± on the highlighted...i thought we are taking absolute value of ##\dfrac{dy}{dx}## which would be a positive.
i.e Arc length = $$\int_a^b \sqrt{1+\left[f^{'}(x)\right]^2} dx$$
 Thanks.
Thanks.
Part (a) is pretty straight forward...No issue here...one has to use chain rule...
Let ##U=\dfrac{e^x+1}{e^x-1}## to realize ##\dfrac{du}{dx}=\dfrac{-2e^x}{(e^x-1)^2}##
and let
##y=\ln u## on taking derivatives, we shall have ##\dfrac{dy}{du}=\dfrac{e^x-1}{e^x+1}##
therefore,
##\dfrac{dy}{dx}=\dfrac{e^x-1}{e^x+1}×\dfrac{-2e^x}{(e^x-1)^2}=-\dfrac{2e^x}{(e^{2x}-1)^2}##Now my question (reason for posting this problem is on part b). Why do we have ± on the highlighted...i thought we are taking absolute value of ##\dfrac{dy}{dx}## which would be a positive.
i.e Arc length = $$\int_a^b \sqrt{1+\left[f^{'}(x)\right]^2} dx$$
Last edited: