paulimerci
- 287
- 47
- Homework Statement
- Question posted below.
- Relevant Equations
- E = kq/r^2
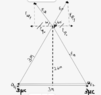
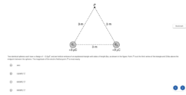
There are two identical spheres with the same charge that are the vertices of an equilateral triangle. ##+3 \mu C## will exert an outward electric field, which is drawn in the FBD below (see the attached pic), Since the horizontal force components (1x and 2x) are equal and opposite at point P, we can cancel those two vectors, and the remaining y component vectors will give the resultant magnitude of the electric field at point P.
$$ E = \frac {kq}{r^2}$$
$$ E_{1y} = \frac {8.99 \times 10^9 \times 3 \times 10^-6 sin 60} {6.76}$$
$$ E_{1y} = 3455 N/C$$
$$E_{2y} = \frac {8.99 \times 10^9 \times 3 \times 10^-6 sin 60} {6.76}$$
$$ E_{2y} = 3455 N/C$$
$$ E _{net} = 6910 N/C$$
I'm not sure where I made a mistake because none of the answers match my answer. Can anyone point out where my mistake is?
$$ E = \frac {kq}{r^2}$$
$$ E_{1y} = \frac {8.99 \times 10^9 \times 3 \times 10^-6 sin 60} {6.76}$$
$$ E_{1y} = 3455 N/C$$
$$E_{2y} = \frac {8.99 \times 10^9 \times 3 \times 10^-6 sin 60} {6.76}$$
$$ E_{2y} = 3455 N/C$$
$$ E _{net} = 6910 N/C$$
I'm not sure where I made a mistake because none of the answers match my answer. Can anyone point out where my mistake is?