anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
Hi members of the forum,
Problem:
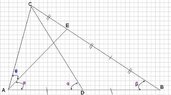
In triangle ABC, D is the midpoint of AB and E is the point of trisection of BC nearer to C. Given that $\displaystyle \angle ADC=\angle BAE$, find $\displaystyle\angle BAC$.
I have tried to solve it using only one approach, that is by assigning $\displaystyle\theta$ and $\displaystyle\beta$ to represent the angles of CAE and ABC respectively and applied the rules of Sine and Cosine appropriately but ended up with very messy equation with many unknown values.
View attachment 630
It's not that I didn't try it but now I feel like I've reached a plateau and I decided to ask for help at MHB.
If anyone could give me some hints, that would be great.
Thanks in advance.
Problem:
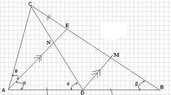
In triangle ABC, D is the midpoint of AB and E is the point of trisection of BC nearer to C. Given that $\displaystyle \angle ADC=\angle BAE$, find $\displaystyle\angle BAC$.
I have tried to solve it using only one approach, that is by assigning $\displaystyle\theta$ and $\displaystyle\beta$ to represent the angles of CAE and ABC respectively and applied the rules of Sine and Cosine appropriately but ended up with very messy equation with many unknown values.
View attachment 630
It's not that I didn't try it but now I feel like I've reached a plateau and I decided to ask for help at MHB.
If anyone could give me some hints, that would be great.
Thanks in advance.