- #1
anemone
Gold Member
MHB
POTW Director
- 3,883
- 115
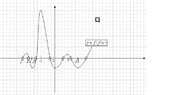
Let $f(x)=x^3-3x+1$. Find the number of distinct real roots of the equation $f(f(x))=0$.