Find the possible values of angle ##∠ADB##

[chwala]

Homework Statement

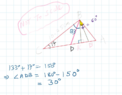
See attached ( kindly allow me to post as it is on exam script)

Relevant Equations

Understanding of the Triangle

My take:

I got $BC=10.25$ cm, using cosine rule...no issue there. For part (b)
$BK=3cm$ using sine rule i.e $\sin 30^0 =\dfrac{BK}{6}$
Thus it follows that $∠BDK=48.59^0$ ...⇒$∠ADB=131.4^0$ correct...any other approach?

Also:

$∠ADB=48.59^0$ when BD is on the other side of the given perpendiculor line.

cheers guys

 

[BvU]

Seem ok to me.
'Not to scale' is an understatement....

And instead of outcomes, post steps: $\angle ADB = \arcsin 3/4 = ...$ is so much clearer !

$\LaTeX$ degrees is ^\circ : $30^\circ$

$\$

 

[SammyS]

Seem ok to me.
'Not to scale' is an understatement....

And instead of outcomes, post steps: $\angle ADB = \arcsin 3/4 = ...$ is so much clearer !

$\LaTeX$ degrees is ^\circ : $30^\circ$

$\$

@chwala ,

In case you miss @BvU 's post, it bears repeating... on all counts.