- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Find the power series in x-x0?
- Thread starter Math10
- Start date
-
- Tags
- Power Power series Series
In summary: please do not provide full solutions to homework problems, just hints that lead the student to the solution.
Physics news on Phys.org
- #2
Math10
- 301
- 0
What I did was the substitution method using z=x-x0.
The answer for this problem is
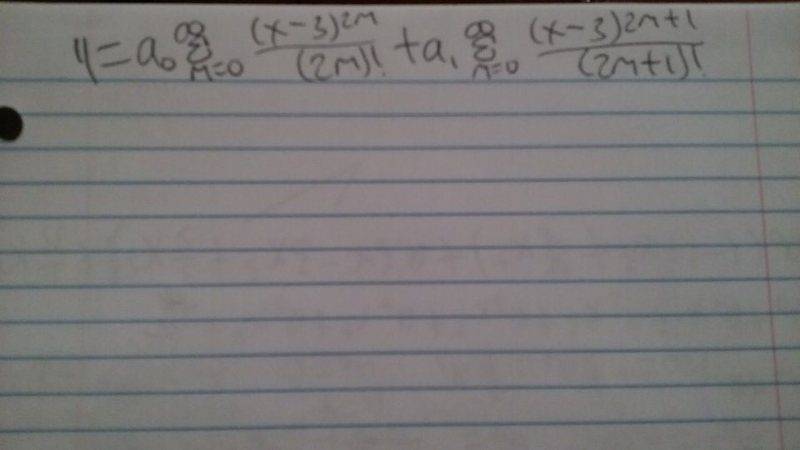
The answer for this problem is
- #3
Ray Vickson
Science Advisor
Homework Helper
Dearly Missed
- 10,704
- 1,723
Math10 said:Homework Statement
Find the power series in x-x0 for the general solution of y"-y=0; x0=3.
Homework Equations
None.
The Attempt at a Solution
Let me post my whole work:
No, please don't. The PF standard is for you to type out the problem and the solution, reserving images for things like diagrams or geometric constructions, etc.
I know that some helpers answer questions about handwritten solution images, but most will not bother. You should consult the pinned post "guidelines for Students and Helpers", by Vela, for a good explanation about this and similar issues.
- #4
Math10
- 301
- 0
Can you please take a look at the work that I posted? It's clearly written.
- #5
- 27,898
- 19,386
Math10 said:Can you please take a look at the work that I posted? It's clearly written.
It looks like the right answer in post #2, if that's all you are asking.
- #6
Math10
- 301
- 0
I know that's the right answer, but what should I do to get to the right answer after the last step in my work? That's where I got stucked.
- #7
- 27,898
- 19,386
Math10 said:I know that's the right answer, but what should I do to get to the right answer after the last step in my work? That's where I got stucked.
You need to spot a pattern in the coefficients (and verify it by induction if need be). You can see from the answer that you need to separate ##n## even and odd.
- #8
Math10
- 301
- 0
You mean this:
n=2m (even index)
a2m+2=a2m/[(2m+2)(2m+1)]
----------------------------------------------------------------------------
n=2m+1 (odd index)
a2m+3=a2m+1/[(2m+3)(2m+2)]
n=2m (even index)
a2m+2=a2m/[(2m+2)(2m+1)]
----------------------------------------------------------------------------
n=2m+1 (odd index)
a2m+3=a2m+1/[(2m+3)(2m+2)]
- #9
- 27,898
- 19,386
Math10 said:You mean this:
n=2m (even index)
a2m+2=a2m/[(2m+2)(2m+1)]
----------------------------------------------------------------------------
n=2m+1 (odd index)
a2m+3=a2m+1/[(2m+3)(2m+2)]
Yes, but can you see the pattern? The answer gives you a big clue!
- #10
Math10
- 301
- 0
So how do I get to the answer? I know where x-3 comes from.
- #11
- 27,898
- 19,386
Math10 said:So how do I get to the answer? I know where x-3 comes from.
You get to the answer by noticing that ##1 \times 2 \times 3 \times \dots \times n = n!##
The clue was that the answer has ##n!## in it.
- #12
Math10
- 301
- 0
I still don't really get it.
- #13
- 27,898
- 19,386
Math10 said:I still don't really get it.
You have:
##(n+2)(n+1)a_{n+2} = a_n##
Hence:
##a_{n+2} = \frac{a_n}{(n+2)(n+1)}##
For ##n## even this gives:
##a_2 = \frac{a_0}{2}, \ a_4 = \frac{a_2}{12} = \frac{a_0}{24}, \ a_6 = \frac{a_4}{30} = \frac{a_0}{720} \dots##
And, now by insight, inspiration (or looking at the answer) you have to notice that ##2, 24, 720 \dots## are the even factorials and hence ##a_n = \frac{a_0}{n!}##
Odd ##n## is much the same.
- #14
Math10
- 301
- 0
I got it now. Thank you so much.
- #15
berkeman
Mentor
- 68,275
- 21,968
This thread is in the Homework Help forums...PeroK said:You have:
##(n+2)(n+1)a_{n+2} = a_n##
Hence:
##a_{n+2} = \frac{a_n}{(n+2)(n+1)}##
For ##n## even this gives:
##a_2 = \frac{a_0}{2}, \ a_4 = \frac{a_2}{12} = \frac{a_0}{24}, \ a_6 = \frac{a_4}{30} = \frac{a_0}{720} \dots##
And, now by insight, inspiration (or looking at the answer) you have to notice that ##2, 24, 720 \dots## are the even factorials and hence ##a_n = \frac{a_0}{n!}##
Odd ##n## is much the same.
FAQ: Find the power series in x-x0?
What is a power series in terms of mathematics?
A power series in mathematics is an infinite series of the form ∑n=0∞ cn(x-x0)n, where cn are coefficients and x0 is a constant. It is used to represent a function as a sum of infinitely many terms involving powers of (x-x0).
How is a power series useful in scientific research?
Power series are useful in scientific research because they can be used to approximate functions that are difficult to evaluate or solve analytically. They are also used in many branches of mathematics, such as calculus and differential equations.
What is the process for finding the power series in x-x0?
The process for finding the power series in x-x0 involves expanding the function into an infinite series by using the Taylor series expansion formula and then simplifying the terms to match the format of a power series. The coefficients can then be calculated using various methods, such as differentiation or integration.
What are the applications of power series in real-world problems?
Power series have many applications in real-world problems, such as in physics, engineering, and economics. They are used to model and approximate various phenomena, such as motion, heat transfer, and population growth.
Are there any limitations to using power series in scientific calculations?
There are some limitations to using power series in scientific calculations. They can only approximate functions within a certain radius of convergence, and the accuracy of the approximation decreases as you move further away from the center point. Additionally, power series may not converge for all values of x, making them unsuitable for certain types of functions.
Similar threads
- Replies
- 68
- Views
- 4K
- Replies
- 3
- Views
- 1K
- Replies
- 2
- Views
- 1K
- Replies
- 4
- Views
- 1K
- Replies
- 6
- Views
- 2K
- Replies
- 7
- Views
- 1K
- Replies
- 8
- Views
- 2K
- Replies
- 22
- Views
- 4K
- Replies
- 1
- Views
- 1K
- Replies
- 5
- Views
- 1K
Share:
