PainterGuy
- 938
- 73
- Homework Statement
- Where am I going wrong with finding the rank?
- Relevant Equations
- Please check my attempt.
Hi,
I was trying to find the rank of following matrix.
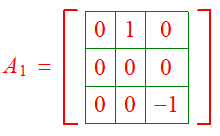
I formed the following system and it seems like all three columns are linearly independent and hence the rank is 3. But the answer says the rank is '2'. Where am I going wrong? Thanks, in advance!
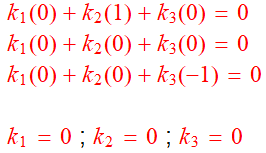
I was trying to find the rank of following matrix.
I formed the following system and it seems like all three columns are linearly independent and hence the rank is 3. But the answer says the rank is '2'. Where am I going wrong? Thanks, in advance!
Last edited by a moderator:


