Find the rejected region in the problem of a biased die - Hypothesis

[chwala]

Homework Statement

Kindly see attached question and mark scheme guide

Relevant Equations

$Bin (n,p)$

Consider the question below:

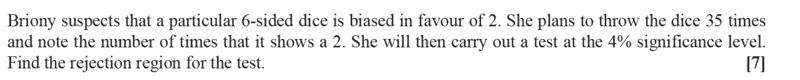
this (below) is the mark scheme for the problem, there were different methods given in the mark scheme but i was interested on this one only...

Now onto my question, How did they calculate $P(X≥10)$=$1-P(X≤9)$=$0.055$...?

In attempting to understand the question i went ahead and looked at a similar problem (attached below); i.e

and i could see from my analysis that, the highlighted value could have been found using the steps below:
$P(x≥4)=1- [ P(x=0) +P(x=1)+P(x=2)+P(x=3)]$
=$1- [0.1615+0.3230+0.2907+0.1550]$
=$1-0.9302$
=$0.0698$
ok is this correct? if so going back to our problem, do we use the same approach? or there is a shorter way...
This is the only part that i need clarity. I should be able to come to the deduction on whether to reject or accept null hypothesis.

 

[Orodruin]

Yes, this is the way to compute it.

 

[chwala]

Yes, this is the way to compute it.

Thanks, implying that a student would have a lot of computation work to do (with calculator) to realize $P(X≥10)$ and $P(X≥11)$... and then come to some conclusion... Phew!