Find the RMS current drawn from the 240 Vrms supply

[youmei0426]

Homework Statement

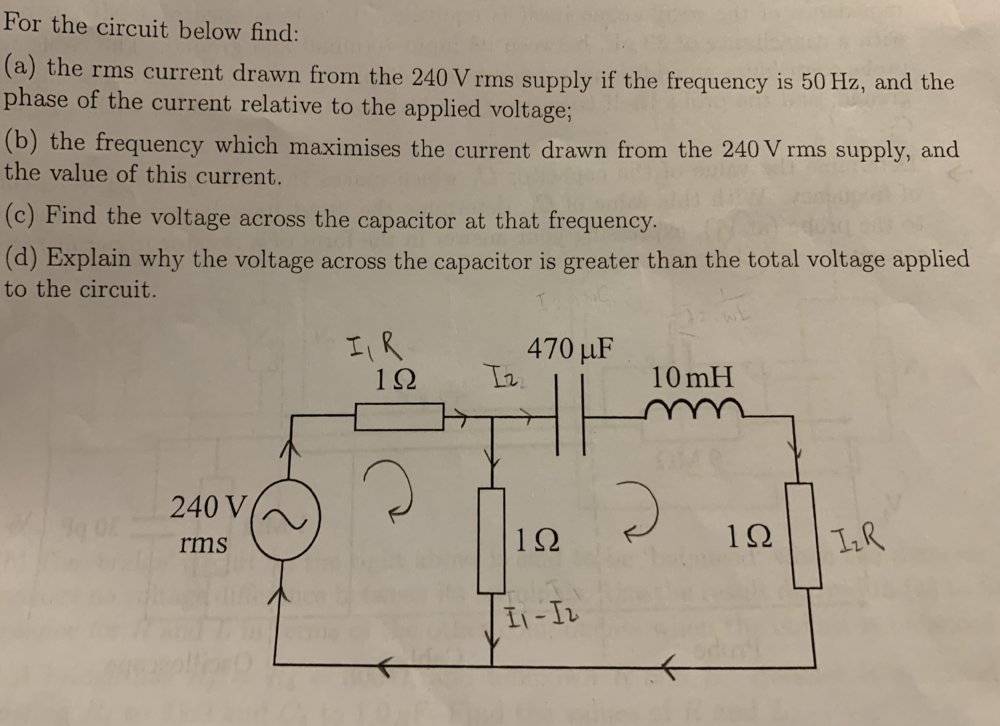
For the circuit below find:
the rms current drawn from the 240 V rms supply if the frequency is 50 Hz, and the phase of the current relative to the applied voltage.

Relevant Equations

Z(R) = R
Z(C) = -i/(wC)
Z(L) = iwL
where Z is complex impedance, R is resistance, w is angular frequency, L is inductance and C is capacitance

My first idea was to find the total impedance of the circuit, but I think viewing the two parallel resistors as one resistor of 0.5 Ohm isn't the correct way? I don't know how to simply this series / parallel circuit further to find Z total.

Then I tried to use Kirchhoff's law to the loop on the left, and got the equation 240 - I₁R - (I₁-I₂)R = 0. Since R = `1, the equation was simplified into
I₂ - 2I₁ + 240 = 0.

Doing the same thing for the loop on the right, and getting the voltages by using IZ, I had the equation
-I₂*(-i/(wC)) - I₂*iwL - I₂ + (I₁ - I₂)=0

Making the real part of the above equation to zero and solving for the two equations, I got I₁ = 160A and I₂ = 80A. However, the answer is supposed to be 126 A with a phase difference of 6.4 degree.

Am I approaching the question in the wrong way?? Thanks in advance for your help!

 

[BvU]

I don't know how to simply this series / parallel circuit further to find Z total.

You don't. You have the left $1 \ \Omega$ in series with a parallel circuit consisting of
$1\ \Omega$ in the left branch and
$\displaystyle {1\over j \omega C} + j\omega L + 1 \ \Omega$ in the right branch.

You need an equation for the complex impedance of this parallel circuit. Simple.

My first idea was to find the total impedance of the circuit

That is indeed what is required

 

[Joshy]

I agree with the first idea (just not the 0.5 Ohms). Equation for a parallel circuit is a good approach, but KCL or KVL should have worked too.

Something in your equations for the right loop doesn't look right to me because you are describing voltages... first terms are voltages, but the last ones are currents. I'm not sure if it's a problem from transcribing or if this is what you put into the calculator (I'm not even sure if it truly is wrong or right I'm just saying my gut feeling is telling me something doesn't look right for the reason of adding currents with voltages). This is the equation that doesn't look right to me (from original post): -I2*(-i/(wC)) - I2*iwL - I2 + (I1 - I2)=0

 

[youmei0426]

You don't. You have the left $1 \ \Omega$ in series with a parallel circuit consisting of
$1\ \Omega$ in the left branch and
$\displaystyle {1\over j \omega C} + j\omega L + 1 \ \Omega$ in the right branch.

You need an equation for the complex impedance of this parallel circuit. Simple.

That is indeed what is required

Ah okay, I will just have to work through the very long equations to find the phase and real part then. Thanks!

 

[youmei0426]

I agree with the first idea (just not the 0.5 Ohms). Equation for a parallel circuit is a good approach, but KCL or KVL should have worked too.

Something in your equations for the right loop doesn't look right to me because you are describing voltages... first terms are voltages, but the last ones are currents. I'm not sure if it's a problem from transcribing or if this is what you put into the calculator (I'm not even sure if it truly is wrong or right I'm just saying my gut feeling is telling me something doesn't look right for the reason of adding currents with voltages). This is the equation that doesn't look right to me (from original post): -I2*(-i/(wC)) - I2*iwL - I2 + (I1 - I2)=0

Ah since the impedance is equal to the resistance which is 1 Ohm in both cases, I wrote just I2 and (I1-I2) instead of I2*R and (I1-I2)*R. Sorry should have made that clearer!

 

[Joshy]

No need to be sorry. I should have noticed it was 1 Ohm :) Thanks!