Find the tension in the two strings

[chwala]

Homework Statement:

See attached;

Relevant Equations:

Mechanics

This is an exam question - refreshing as usual.

Literature Overview;
In the free-body diagram shown above, we can see the horizontal and vertical components of the tension forces, T₁, and T₂. Forces are vectors, which means they always have both magnitudes and directions. Like all vectors, forces can be expressed in these components, which give the force's influence along the horizontal and vertical axes. T₁ₓ and T₂ₓ are the horizontal components of T₁ and T₂, respectively. On the other hand, T1y and T2y are the vertical components of the same forces, respectively. Since gravity acts on the object in the vertical axis, we need to consider the tension forces' vertical components for our summation of forces as follows:

$ΣF↑ = 0 = T_1 y + T_2 y + (-W)$

$T=W$ where $T=T_1 y + T_2 y$

$16 = T_1 \sin 40^0 + T_2 \sin 20^0$

We can also say that for the system to be in equilibrium, the object should not move horizontally or along the x-axis. Therefore, the horizontal components of T₁ and T₂ must then equate to zero. Also, with the help of trigonometry, we can express T₁ₓ and T₂ₓ in terms of T₁ and T₂, respectively:

$T_1 x = T_2 x$

$T_1 \cos 40^0 =T_2 \cos 20^0$

Therefore we shall have the simultaneous equation;

$16 = T_1 \sin 40^0 + T_2 \sin 20^0$

$T_1 \cos 40^0 =T_2 \cos 20^0$, Where;

$T_1=\dfrac{T_2 \cos 20^0}{\cos 40^0}$

Substituting on;

$16 = T_1 \sin 40^0 + T_2 \sin 20^0$, we shall have

$16=\dfrac {T_2 \sin 40^0 \cos 20^0}{\cos 40^0} + T_2 \sin 20^0$

$T_2(0.7885+0.342)=16$

$T_2 = 14.153$ to 3 decimal places.

$T_1=\dfrac{14.153 ×\cos 20^0}{\cos 40^0}=17.361$ to three decimal places.



Find mark scheme solution here;

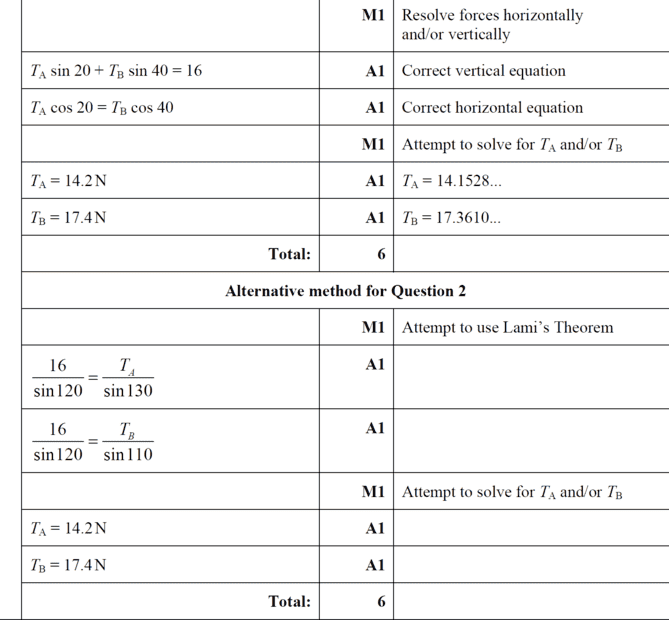Your insight is welcome.

 

[Steve4Physics]

In the free-body diagram shown above,

The diagram shown is not a free body diagram.

we can see the horizontal and vertical components of the tension forces, T₁, and T₂. Forces are vectors, which means they always have both magnitudes and directions. Like all vectors, forces can be expressed in these components, which give the force's influence along the horizontal and vertical axes. T₁ₓ and T₂ₓ are the horizontal components of T₁ and T₂, respectively. On the other hand, T1y and T2y are the vertical components of the same forces, respectively. Since gravity acts on the object in the vertical axis, we need to consider the tension forces' vertical components for our summation of forces as follows:

The long explanation is unnecessary. Look at the mark scheeme - there are no marks associated with the explanation. In an examination, this would cost you valuable time for zero benefit.

We can also say that for the system to be in equilibrium, the object should not move horizontally or along the x-axis.

This is irrelevant. The question tells you that the object is in equlibrium. (In any case, an object can be moving and still be in equlibrium - providing its velocity is constant.)

Therefore, the horizontal components of T₁ and T₂ must then equate to zero. Also, with the help of trigonometry, we can express T₁ₓ and T₂ₓ in terms of T₁ and T₂, respectively:

You don't need to say all that.

$T_1 x = T_2 x$

To be consistant with your approach to the vertical components, you should write
$T_1 x + T_2 x = 0$

$T_2 = 14.153$ to 3 decimal places.
$T_1=\dfrac{14.153 ×\cos 20^0}{\cos 40^0}=17.361$ to three decimal places.

If these are intended as final answers, you have forgotten the units and 3 decimal places is unjustifiable.

Your understanding is good but (IM O) you should make your answers far more concise.

And note that Lami's method is much simpler!

 

[chwala]

The diagram shown is not a free body diagram.


The long explanation is unnecessary. Look at the mark scheeme - there are no marks associated with the explanation. In an examination, this would cost you valuable time for zero benefit.


This is irrelevant. The question tells you that the object is in equlibrium. (In any case, an object can be moving and still be in equlibrium - providing its velocity is constant.)


You don't need to say all that.


To be consistant with your approach to the vertical components, you should write
$T_1 x + T_2 x = 0$


If these are intended as final answers, you have forgotten the units and 3 decimal places is unjustifiable.

Your understanding is good but (IM O) you should make your answers far more concise.

And note that Lami's method is much simpler!

@Steve4Physics thanks...kindly note that the literature (copy pasted from google) is only for my reference and future review of my own posts...my interest is solely on the understanding of the concept as it has been long since attempting these questions...feedback noted though- thanks mate.

 

[Steve4Physics]

:chwa

@Steve4Physics thanks...kindly note that the literature (copy pasted from google) is only for my reference and future review of my own posts...my interest is solely on the understanding of the concept as it has been long since attempting these questions...feedback noted though- thanks mate.

My apologies @chwala. I thought you had written the solution. Do you understand it? Or is there something you are struggling with?

 

[chwala]

:chwa

My apologies @chwala. I thought you had written the solution. Do you understand it? Or is there something you are struggling with?

I understand it...

I am just but refreshing ...I majorly teach Maths ...though in my undergraduate degree i did Physics (minor)... always good to refresh on the concepts. An interesting area was Electromagnetism, Polymer physics...cheers mate.

 

[Lnewqban]

I would clarify in the solution that the units of weight and tensions are Newtons.
The hanging mass of 1.6 kg becomes 16 N in the initial equation without showing the mg step.

 

[chwala]

I would clarify in the solution that the units of weight and tensions are Newtons.
The hanging mass of 1.6 kg becomes 16 N in the initial equation without showing the mg step.

Yes, that's pretty straightforward; we use $w=mg$. Where $g=10$ m/s^2.

 

[Lnewqban]

Yes, that's pretty straightforward; we use $w=mg$.

Also, it may be useful to mention to the students that in practical terms, the angles could never be zero, because the magnitudes of the tensions would be infinite and either the rope/chain/cable or the anchors would fail.